logo

TE. Arithmétique : divisions et congruences.

Congruences

Définition

On dit que a et b sont congrus modulo n signifie que a et b ont le même reste dans la division euclidienne par n.

On note  a\equiv b[n] ou a\equiv b(modn)

Exemple n°1 :

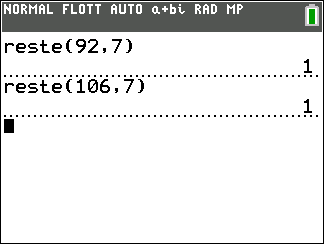
92 et 106 sont congrus modulo 7 car 92 et 106 ont le même reste : 1 dans la division euclidienne par 7.

On note  92\equiv 106[7]

Illustration avec la TI 83 Premium CE Python :

Exemple n°2 :

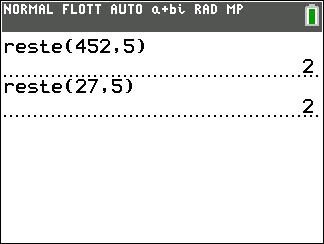
452 et 27 sont congrus modulo 5 car 452 et 27 ont le même reste : 2 dans la division euclidienne par 5.

On note  452\equiv 27[5]

Illustration avec la TI 83 Premium CE Python :

Conséquences

a\equiv a[n]

si  a\equiv b[n] alors  b\equiv a[n]

si  a\equiv b[n] et b\equiv c[n] alors a\equiv c[n].

si  r est le reste de la division de a par b alors a \equiv r[n].

a\equiv 0[n] si et seulement si  a est divisible par a.

Propriété

a\equiv b[n] si et seulement si  a-b est un multiple de n.

Démonstration

Si a\equiv b[n] alors il existe des entiers relatifs  q , q’  et r tels que a=nq+r et b=nq’+r avec 0\leq r<n.

On soustrait les deux égalités :

a-b=nq+r-nq’-r\\a-b=nq-nq’\\a-b=n(q-q’) donc a-b est un multiple de n.

Réciproquement, si a-b est un multiple de n alors il existe un entier relatif k tel que  a-b=kn ou a=b+kn.

Si on divise b par n, on obtient b=n\times q’+r’ avec 0\leq r'<n.

On remplace b par n\times q’+r’ dans a=b+kn.

a=n\times q’+r’+kn

a=n(q’+k)+r’ avec 0\leq r'<n.

Donc r’ est aussi le reste de la division de a par n.

Donc a et b ont le même reste r’ dans leur division par n.

Donc a\equiv b[n].

Propriétés

Si a\equiv b[n] et c\equiv d[n] alors :

a+c\equiv b+d[n]\\a-c\equiv b-d[n]\\ac\equiv bd[n]

Pout tout p\in \mathbf{N} , a^p\equiv b^p[n] 

Exemple n°3 :

a et b sont deux entiers tels que a\equiv7[13] et b\equiv4[13]

  1. Donner le reste de la division euclidienne par 13 de a+b.

On utilise la propriété Si a\equiv b[n] et c\equiv d[n] alors a+c\equiv b+d[n].

a\equiv7[13] et b\equiv4[13] donc a+b\equiv7+4[13]\\a+b\equiv11[13], comme 0\leq 11<13, le reste de la division de a+b par 13 est 11.

2.Donner le reste de la division euclidienne par 13 de a-b.

On utilise la propriété Si a\equiv b[n] et c\equiv d[n] alors a-c\equiv b-d[n].

a\equiv7[13] et b\equiv4[13] donc a-b\equiv7-4[13]\\a-b\equiv 3[13], comme 0\leq 3<13, le reste de la division de a-b par 13 est 3.

3.Donner le reste de la division euclidienne par 13 de ab.

On utilise la propriété Si a\equiv b[n] et c\equiv d[n] alors ac\equiv bd[n].

a\equiv7[13] et b\equiv4[13] donc ab\equiv7\times4[13]\\ab\equiv 28[13], comme 28>13, il faut diviser 28 par 13.

28=2\times 13+2 donc le reste de la division de 28 par 13 est 2.

Comme ab\equiv 28[13], ils ont même reste dans la division par 13, donc le reste de la division de ab par 13 est 2

4.Donner le reste de la division euclidienne par 13 de a^2.

On utilise la propriété Si a\equiv b[n] alors a^2\equiv b^2[n].

a\equiv7[13] donc a^2\equiv7^2[13]\\a^2\equiv 49[13], comme 49>13, il faut diviser 49 par 13.

49=3\times 13+10 donc le reste de la division de 49 par 13 est 10.

Comme a^2\equiv 28[13], ils ont même reste dans la division par 13, donc le reste de la division de a^2 par 13 est 10

Exemple n°4 : tableau de congruence

  1. Reproduire et compléter (en rouge) le tableau de congruence modulo 3 ci-dessous où n représente un entier relatif.
n\equiv…[3]n\equiv 0n\equiv 1n\equiv 2[3]
n^2\equiv…[3]n^2\equiv0[3]n^2\equiv 1[3]n^2\equiv 4[3]
2n\equiv…[3]2n\equiv0[3]2n\equiv 2[3]2n\equiv 4[3]
n^2+2n\equiv…[3]n^2+2n\equiv0[3]n^2+2n\equiv 3[3]n^2+2n\equiv8[3]

2. Déterminer alors les restes de la division de n^2+2n par 3.

Compte-tenu de la dernière ligne du tableau, on constate que les restes seront : 0 ou 2.

En effet on a n^2+2n\equiv 3[3] et 3\equiv 0[3] donc n^2+2n\equiv 0[3].

Et on a n^2+2n\equiv 8[3] et 8\equiv 2[3] donc n^2+2n\equiv 2[3].

Exercice n°1

a et b sont deux entiers tels que a\equiv 6[11] et b\equiv 4[11]

  1. Donner le reste de la division euclidienne par 11 de a+b.
correction

2. Donner le reste de la division euclidienne par 11 de a-b.

correction

3. Donner le reste de la division euclidienne par 11 de ab.

correction

4. Donner le reste de la division euclidienne par 11 de 5a.

correction

5. Donner le reste de la division euclidienne par 11 de a^3.

correction

Exercice n°2

a et b sont deux entiers tels que a\equiv 2[7] et b\equiv 5[7]

  1. Donner le reste de la division euclidienne par 7 de a+b.
correction

2. Donner le reste de la division euclidienne par 7 de a-b.

correction

3. Donner le reste de la division euclidienne par 7 de ab.

correction

4. Donner le reste de la division euclidienne par 7 de 4a.

correction

5. Donner le reste de la division euclidienne par 7 de a^3.

correction

Exercice n°3

  1. x désigne un nombre entier relatif, démontrer que si x n’est pas un multiple de 3 , alors x^2\equiv 1[3].
correction

2. Démontrer que pour tous entiers relatifs a et b , le nombre  N=ab(a^2-b^2) est divisible par 3

correction

Exercice n°4

  1. Démontrer que 5^2\equiv -1[13] puis que 5^4\equiv 1[13]
correction

2. n désigne un nombre entier naturel, démontrer que 5^{4n}\equiv 1[13].

correction

Exercice n°5

Déterminer le reste de la division par  7 de 78^{115}+92^{23}+106^{35}.

correction

Exercice n°6

On donne A=877+59^{43} . On souhaite déterminer le reste de la division euclidienne de A par 7.

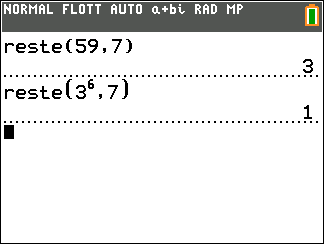
  1. Justifier que  59\equiv 3[7] et que 3^6\equiv 1[7].
j'utilise ma TI 83 Premium CE Python
correction 59\equiv 3[7]
correction 3^6\equiv 3[7]

2. Effectuer la division de 43 par 6 et en déduire que 3^{43}\equiv 3[7].

correction

3. Quel est finalement le reste cherché ?.

correction

Exercice n°7

n désigne un nombre entier naturel.

Déterminer les restes de la division euclidienne de :

n^2 par 5

correction

n^2 par 7

correction

n^3 par 5

correction

n^3 par 7

correction

Exercice n°8 :

A l’aide d’un tableau de congruences et de la calculatrice, démontrer que pour tout nombre entier naturel n, 

 n^7+6n\equiv0[7].

correction

©2020 – Math’O karé SAS

a et b sont deux entiers tels que a\equiv6[11] et b\equiv4[11]

On cherche le reste de la division euclidienne par 11 de a+b.

On utilise la propriété Si a\equiv b[n] et c\equiv d[n] alors a+c\equiv b+d[n].

a\equiv6[11] et b\equiv4[11] donc a+b\equiv6+4[11]\\a+b\equiv10[11], comme 0\leq 10<11, le reste de la division de a+b par 11 est 10.

 

a et b sont deux entiers tels que a\equiv6[11] et b\equiv4[11]

On cherche le reste de la division euclidienne par 11 de a-b.

On utilise la propriété Si a\equiv b[n] et c\equiv d[n] alors a-c\equiv b-d[n].

a\equiv6[11] et b\equiv4[11] donc a-b\equiv6-4[11]\\a+b\equiv2[11], comme 0\leq 2<11, le reste de la division de a-b par 11 est 2.

a et b sont deux entiers tels que a\equiv6[11] et b\equiv4[11]

On cherche le reste de la division euclidienne par 11 de ab.

On utilise la propriété Si a\equiv b[n] et c\equiv d[n] alors ac\equiv bd[n].

a\equiv6[11] et b\equiv4[11] donc ab\equiv6\times 4[11]\\a+b\equiv24[11], comme 24>11, il faut diviser 24 par 11.

24=2\times 11+2 donc le reste de la division de 24 par 11 est 2.

Comme ab\equiv 24[11], ils ont même reste dans la division par 11, donc le reste de la division de ab par 11 est 2

a et b sont deux entiers tels que a\equiv6[11] et b\equiv4[11]

On cherche le reste de la division euclidienne par 11 de 5a.

On utilise la propriété Si a\equiv b[n] et c\equiv d[n] alors ac\equiv bd[n].

a\equiv6[11]  donc 5a\equiv5\times 6[11]\\5a\equiv30[11], comme 30>11, il faut diviser 30 par 11.

30=2\times 11+8 donc le reste de la division de 30 par 11 est 8.

Comme 5a\equiv 30[11], ils ont même reste dans la division par 11, donc le reste de la division de 5a par 11 est 8.

a et b sont deux entiers tels que a\equiv6[11] et b\equiv4[11]

On cherche le reste de la division euclidienne par 11 de a^3.

On utilise la propriété Si a\equiv b[n] alors a^3\equiv b^3[n].

a\equiv6[11] donc a^3\equiv6^3[11]\\a^3\equiv 216[11], comme 216>11, il faut diviser 216 par 11.

216=19\times 11+7 donc le reste de la division de 216 par 19 est 7.

Comme a^3\equiv 216[11], ils ont même reste dans la division par 11, donc le reste de la division de a^3 par 11 est 7.

a et b sont deux entiers tels que a\equiv2[7] et b\equiv5[7]

On cherche le reste de la division euclidienne par 7 de a+b.

On utilise la propriété Si a\equiv b[n] et c\equiv d[n] alors a+c\equiv b+d[n].

a\equiv2[7] et b\equiv5[7] donc a+b\equiv2+5[7]\\a+b\equiv7[7], comme 7 n’est pas strictement plus petit que le diviseur 7, il faut diviser 7 par 7.

7=1\times 7+0 donc le reste de la division de 7 par 7 est 0.

Comme a+b\equiv 7[7], ils ont même reste dans la division par 7, donc le reste de la division de a+b par 7 est 0.

a et b sont deux entiers tels que a\equiv2[7] et b\equiv5[7]

On cherche le reste de la division euclidienne par 7 de a-b.

On utilise la propriété Si a\equiv b[n] et c\equiv d[n] alors a-c\equiv b-d[n].

a\equiv2[7] et b\equiv5[7] donc a-b\equiv2-5[7]\\a-b\equiv-3[7], comme -3 est négatif, il ne peut pas être le reste et il faut diviser -3 par 7.

-3=-1\times 7+4 donc le reste de la division de -3 par 7 est 4.

Comme a-b\equiv -3[7], ils ont même reste dans la division par 7, donc le reste de la division de a-b par 7 est 4.

a et b sont deux entiers tels que a\equiv2[7] et b\equiv5[7]

On cherche le reste de la division euclidienne par 7 de ab.

On utilise la propriété Si a\equiv b[n] et c\equiv d[n] alors ac\equiv bd[n].

a\equiv2[7] et b\equiv5[7] donc ab\equiv2 \times5[7]\\ab\equiv10[7], comme 10>7, il ne peut pas être le reste et il faut diviser 10 par 7.

10=1\times 7+3 donc le reste de la division de 10 par 7 est 3.

Comme ab\equiv 10[7], ils ont même reste dans la division par 7, donc le reste de la division de ab par 7 est 3.

a et b sont deux entiers tels que a\equiv2[7] et b\equiv5[7]

On cherche le reste de la division euclidienne par 7 de 4a.

On utilise la propriété Si a\equiv b[n] et c\equiv d[n] alors ac\equiv bd[n].

a\equiv2[7] et 4\equiv4[7] donc 4a\equiv2 \times4[7]\\4a\equiv8[7], comme 8>7, il ne peut pas être le reste et il faut diviser 8 par 7.

8=1\times 7+1 donc le reste de la division de 8 par 7 est 1.

Comme 4a\equiv 8[7], ils ont même reste dans la division par 7, donc le reste de la division de 4a par 7 est 1.

a et b sont deux entiers tels que a\equiv2[7] et b\equiv5[7]

On cherche le reste de la division euclidienne par 7 de a^3.

On utilise la propriété Si a\equiv b[n] alors a^3\equiv b^3[n].

a\equiv2[7] donc a^3\equiv2^3[7]\\a^3\equiv 8[7], comme 8>7, il faut diviser 8 par 7.

8=1\times 7+1 donc le reste de la division de 8 par 7 est 1.

Comme a^3\equiv 8[7], ils ont même reste dans la division par 7, donc le reste de la division de a^3 par 7 est 1.

Si x n’est pas un multiple de 3 alors x\equiv 1[3] ou x\equiv 2[3].

cas n°1 : x\equiv 1[3] donc x^2\equiv 1[3] 

cas n°2 : x\equiv 2[3] donc x^2\equiv 4[3] , comme 4\equiv 1[3] alors x^2\equiv 1[3]

Ainsi si x n’est pas un multiple de 3 alors x^2\equiv 1[3].

On veut montrer que pour tous entiers relatifs a et b , le nombre  N=ab(a^2-b^2) est divisible par 3

cas n°1 : si a ou b est un multiple de 3 alors le produit ab est un multiple de  3 et donc N est un multiple de  3.

cas n°2 : si a et b ne sont pas des multiples de 3, d’après la question n°1, on a :

a^2\equiv 1[3] et b^2\equiv 1[3] donc a^2-b^2\equiv 1-1[3] ou a^2-b^2\equiv 0[3].

Donc a^2-b^2 est un multiple de  3 et donc N est un multiple de  3.

Ainsi pour tous entiers relatifs a et b , le nombre  N=ab(a^2-b^2) est divisible par 3.

1. On veut montrer que  5^2\equiv -1[13].

On fait la division euclidienne de 25 par 13.

25=1\times 13+12\\25\equiv  12[13]

On fait la division euclidienne de -1 par 13.

-1=-1\times 13+12\\-1\equiv  12[13]

Donc 5^2\equiv -1[13]

2. On veut montrer que  5^4\equiv 1[13].

Comme 5^2\equiv -1[13]

On élève au carré.

(5^2)^2\equiv (-1)^2[13]

Donc : 5^4\equiv 1[13]

 

D’après la question n°1 :

5^4\equiv 1[13]

On élève à la puissance n.

(5^4)^n\equiv 1^n[13]

Donc : 5^{4n}\equiv 1[13].

On veut déterminer le reste de la division par  7 de 78^{115}+92^{23}+106^{35}.

On va déterminer d’abord les restes de 78 ; 92;106 dans la division par 7.

On fait la division euclidienne de 78 par 7.

78=11\times 7+1\\78\equiv  1[7]

On fait la division euclidienne de 92 par 7.

92=13\times 7+1\\92\equiv  1[7]

On fait la division euclidienne de 106 par 7.

106=15\times 7+1\\106\equiv  1[7]

On applique la propriété suivante : Pout tout p\in \mathbf{N} , a^p\equiv b^p[n] 

78^{115}\equiv  1^{115}[7]\\78^{115}\equiv  1[7]
92^{23}\equiv  1^{23}[7]\\92^{23}\equiv  1[7]
106^{35}\equiv  1^{35}[7]\\106^{35}\equiv  1[7]

On applique la propriété suivante : si a\equiv b[n] et c\equiv d[n] alors a+c\equiv b+d[n] 

78^{115}+92^{23}+106^{35}\equiv 1+1+1[7]\\78^{115}+92^{23}+106^{35}\equiv 3[7]

Comme 0\leq 3<7, 3 est le reste de la division par  7 de 78^{115}+92^{23}+106^{35}

 

 

On veut montrer que  59\equiv 3[7]

On fait la division euclidienne de 59 par 7.

59=8\times 7+3\\59\equiv  3[7]

On veut montrer que  3^6\equiv 1[7]

On fait la division euclidienne de 3^6=729 par 7.

729=104\times 7+1\\729\equiv  1[7]

On effectue la division de 43 par 6.

43=7\times6+1

On en déduit que 3^{43}\equiv 3[7].

On a vu que 

3^{6}\equiv 1[7]

(3^{6})^7\equiv 1^7[7]

3^{6\times7}\equiv 1[7]

3\times 3^{6\times7}\equiv 3\times 1[7]

3^{6\times7+1}\equiv 3[7]

3^{43}\equiv 3[7]

On effectue la division de 877 par 7.

877=125\times7+2

Donc 877\equiv 2[7]

 

On a vu que :

59\equiv 3[7]

Donc 59^{43}\equiv 3^{43}[7]

On a montré précédemment que 3^{43}\equiv 3[7].

Donc 59^{43}\equiv 3[7]

Donc, par somme :

877+59^{43}\equiv 2+3[7]

877+59^{43}\equiv 5[7]

Ainsi le reste de la division de 877+59^{43} par 7 est 5

On va utiliser un tableau de congruences :

n\equiv 0[5]

n\equiv 1[5]n\equiv 2[5]n\equiv 3[5]n\equiv 4[5]

n^2\equiv 0[5]

n^2\equiv 1[5]n^2\equiv 4[5]n^2\equiv 9[5]n^2\equiv 16[5]
  • On obtient comme restes 0,1,4 pour les trois premières colonnes.
  • Pour la quatrième colonne, on a n^2\equiv 9[5], comme 9>5, ce n’est pas un reste. on divise 9 par 5 :

9=1\times 5+4 donc le reste est 4.

  • Pour la cinquième colonne, on a n^2\equiv 16[5], comme 16>5, ce n’est pas un reste. on divise 16 par 5 :

16=3\times 5+1 donc le reste est 1.

Ainsi les restes de la division de  n^2 par 5 sont : 0,1,4.

On va utiliser un tableau de congruences :

n\equiv 0[7]n\equiv 1[7]n\equiv 2[7]n\equiv 3[7]n\equiv 4[7]n\equiv 5[7]n\equiv 6[7]
n^2\equiv 0[7]n^2\equiv 1[7]n^2\equiv 4[7]n^2\equiv 9[7]n^2\equiv 16[7]n^2\equiv 25[7]n^2\equiv 36[7]
  • On obtient comme restes 0,1,4 pour les trois premières colonnes.
  • Pour la quatrième colonne, on a n^2\equiv 9[7], comme 9>7, ce n’est pas un reste. On divise 9 par 7 :

9=1\times 7+2 donc le reste est 2.

  • Pour la cinquième colonne, on a n^2\equiv 16[7], comme 16>7, ce n’est pas un reste. On divise 16 par 7 :

16=2\times 7+2 donc le reste est 2.

  • Pour la sixième colonne, on a n^2\equiv 25[7], comme 25>7, ce n’est pas un reste. On divise 25 par 7 :

25=3\times 7+4 donc le reste est 4.

  • Pour la septième colonne, on a n^2\equiv 36[7], comme 36>7, ce n’est pas un reste. On divise 36 par 7

36=5\times 7+1 donc le reste est 1.

 

Ainsi les restes de la division de  n^2 par 7 sont : 0,1,2,4.

On va utiliser un tableau de congruences :

n\equiv 0[5]

n\equiv 1[5]n\equiv 2[5]n\equiv 3[5]n\equiv 4[5]

n^3\equiv 0[5]

n^3\equiv 1[5]n^3\equiv 8[5]n^3\equiv 27[5]n^3\equiv 64[5]
  • On obtient comme restes 0,1 pour les deux premières colonnes.
  • Pour la troisième colonne, on a n^3\equiv 8[5], comme 8>5, ce n’est pas un reste. on divise 8 par 5 :

8=1\times 5+3 donc le reste est 3.

  • Pour la quatrième colonne, on a n^3\equiv 27[5], comme 27>5, ce n’est pas un reste. on divise 27 par 5 :

27=5\times 5+2 donc le reste est 2.

  • Pour la cinquième colonne, on a n^3\equiv 64[5], comme 64>5, ce n’est pas un reste. on divise 64 par 5 :

64=12\times 5+4 donc le reste est 4.

Ainsi les restes de la division de  n^2 par 5 sont : 0,1,2,3,4.

 

On va utiliser un tableau de congruences :

n\equiv 0[7]n\equiv 1[7]n\equiv 2[7]n\equiv 3[7]n\equiv 4[7]n\equiv 5[7]n\equiv 6[7]
n^3\equiv 0[7]n^3\equiv 1[7]n^3\equiv 8[7]n^3\equiv 27[7]n^3\equiv 64[7]n^3\equiv 125[7]n^2\equiv 216[7]
  • On obtient comme restes 0,1 pour les deux premières colonnes.
  • Pour la troisième colonne, on a n^3\equiv 8[7], comme 8>7, ce n’est pas un reste. On divise 8 par 7 :

8=1\times 7+1 donc le reste est 1.

  • Pour la quatrième colonne, on a n^3\equiv 27[7], comme 27>7, ce n’est pas un reste. On divise 27 par 7 :

27=3\times 7+6 donc le reste est 6.

  • Pour la cinquième colonne, on a n^3\equiv 64[7], comme 64>7, ce n’est pas un reste. On divise 64 par 7 :

64=9\times 7+1 donc le reste est 1.

  • Pour la sixième colonne, on a n^3\equiv 125[7], comme 125>7, ce n’est pas un reste. On divise 125 par 7 :

125=17\times 7+6 donc le reste est 6.

  • Pour la septième colonne, on a n^3\equiv 216[7], comme 216>7, ce n’est pas un reste. On divise 216 par 7

216=30\times 7+6 donc le reste est 6.

Ainsi les restes de la division de  n^3 par 7 sont : 0,1,6.

 

 

Utiliser un tableau de congruences.

  1. Pour remplir la deuxième ligne, utiliser la calculatrice. 
n\equiv 0[7]n\equiv 1[7]n\equiv 2[7]n\equiv 3[7]n\equiv 4[7]n\equiv 5[7]n\equiv 6[7]
n^7\equiv 0[7]n^7\equiv 1[7]n^7\equiv 2[7]n^7\equiv 3[7]n^7\equiv 4[7]n^7\equiv 5[7]n^7\equiv 6[7]
       
       

2. Pour remplir la deuxième ligne, utiliser la calculatrice. 

n\equiv 0[7]n\equiv 1[7]n\equiv 2[7]n\equiv 3[7]n\equiv 4[7]n\equiv 5[7]n\equiv 6[7]
n^7\equiv 0[7]n^7\equiv 1[7]n^7\equiv 2[7]n^7\equiv 3[7]n^7\equiv 4[7]n^7\equiv 5[7]n^7\equiv 6[7]
6n\equiv 0[7]6n\equiv 6[7]6n\equiv 5[7]6n\equiv 4[7]6n\equiv 3[7]6n\equiv 2[7]6n\equiv 1[7]
       

3. Pour remplir la troisième ligne, on peut le faire sans difficulté ( remarque 7\equiv 0[7] )

n\equiv 0[7]n\equiv 1[7]n\equiv 2[7]n\equiv 3[7]n\equiv 4[7]n\equiv 5[7]n\equiv 6[7]
n^7\equiv 0[7]n^7\equiv 1[7]n^7\equiv 2[7]n^7\equiv 3[7]n^7\equiv 4[7]n^7\equiv 5[7]n^7\equiv 6[7]
6n\equiv 0[7]6n\equiv 6[7]6n\equiv 5[7]6n\equiv 4[7]6n\equiv 3[7]6n\equiv 2[7]6n\equiv 1[7]
n^7+6n\equiv 0[7]n^7+6n\equiv 0[7]n^7+6n\equiv 0[7]n^7+6n\equiv 0[7]n^7+6n\equiv 0[7]n^7+6n\equiv 0[7]n^7+6n\equiv 0[7]

Donc pour tout nombre entier naturel n,  n^7+6n\equiv0[7].

 

 

Réponse:

\overrightarrow{DC}=\overrightarrow{HG}.

Résoudre graphiquement f(x)=1

C’est une autre façon de demander de déterminer graphiquement les antécédents de 1.

Je place 1 sur l’axe des ordonnées, je trace alors la parallèle à l’axe des abscisses passant par 1 toute entière. Je repère les points d’intersection avec la courbe. Les abscisses de ces points sont les antécédents de 1.

Les antécédents sont -2 et 2.

Donc S=\{-2;2\}

Remarque : comme on demande de résoudre une équation, il faut écrire ainsi l’ensemble des solutions.