Sommaire
Propriété
Soient a, b et c trois entiers relatifs non nuls.
L’équation diophantienne ax+by=c où les inconnues x et y sont des entiers relatifs admet des solutions si et seulement si c est un multiple du PGCD(a;b).
Exemples
- Comme PGCD(14;21)=7, l’équation 14x+21y=28 admet au moins un couple d’entiers solutions car 28 est un multiple de 7.
- Comme PGCD(3;5)=1, l’équation 3x+5y=2 admet au moins un couple d’entiers solutions car 2 est un multiple de 1.
- Comme PGCD(4;6)=2, l’équation 4x+6y=1 n’admet pas de couple d’entiers solutions car 1 n’est pas un multiple de 2.
Exercice n°1
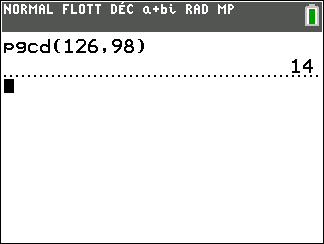
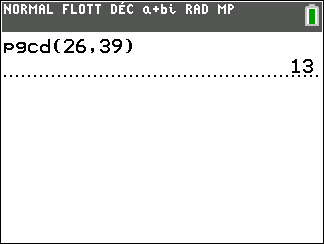
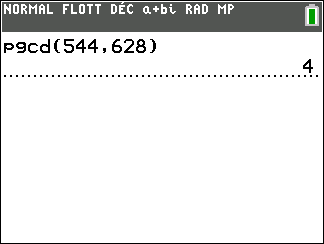
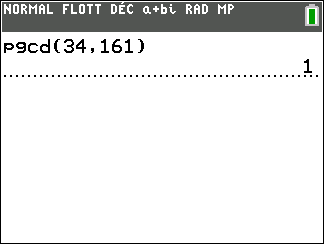
Parmi les équations diophantiennes suivantes, quelles sont celles qui admettent au moins une solution.
On utilisera la calculatrice pour déterminer le PGCD dans chaque cas.
Exercice n°2
Déterminer une solution particulière pour chacune des équations diophantiennes suivantes ( on suppose qu’elles admettent au moins un couple solution ).
Exemple n°1 : résoudre une équation diophantienne
On considère l’équation suivante 4x+3y=2.
1.Démontrer que cette équation admet des solutions.
Comme PGCD(4;3)=1, l’équation 4x+3y=2 admet au moins un couple d’entiers solutions car 2 est un multiple de 1.
2. Déterminer une solution particulière de l’équation.
La méthode à utiliser n’est pas précisée dans la question donc on peut utiliser la méthode de notre choix, par exemple : le calcul mental.
Le couple (2;-2) est solution car 4\times 2+3\times (-2)=8-6=2.
3. Déterminer l’ensemble des couples solutions de cette équation.
On soustrait membre à membre ces deux égalités :
4x+3y=2\\4\times 2+3\times (-2)=2\\4x-4\times 2+3y-3\times (-2)=2-2On réduit
4x-4\times 2+3y-3\times (-2)=0On factorise
4(x-2)+3(y+2)=0\\4(x-2)=-3(y+2)\\4 et 3 sont premiers entre eux donc d’après le théorème de Gauss, 4 divise y+2.
Donc il existe un entier relatif k tel que y+2=4k.
Donc y=4k-2
On remplace y+2 par 4k dans 4(x-2)=-3(y+2).
4(x-2)=-3\times 4k\\x-2=-3k\\x=-3k+2Les couples solutions sont de la forme (-3k+2;4k-2) avec k\in \mathbf{Z}.
On s’assure que les solutions trouvées sont bien solutions de l’équation 4x+3y=2.
4(-3k+2)+3(4k-2)=-12k+8+12k-6=2Exemple n°2 : résoudre une équation diophantienne
On considère l’équation suivante 15x+8y=5.
1.Démontrer que cette équation admet des solutions.
Comme PGCD(15;8)=1, l’équation 15x+8y=5 admet au moins un couple d’entiers solutions car 5 est un multiple de 1.
2.a. Déterminer une solution particulière de l’équation 15x+8y=1
La méthode à utiliser n’est pas précisée dans la question donc on peut utiliser la méthode de notre choix, par exemple : le calcul mental.
Le couple (-1;2) est solution car 15\times (-1)+8\times 2=-15+16=1.
2.b. En déduire une solution particulière de 15x+8y=5.
Dans la question précédente, on a établi que :
15\times (-1)+8\times 2=1On multiplie cette égalité par 5 de chaque côté.
5 \times (15\times (-1)+8\times 2)=5 \times 1\\15\times (-5)+8\times 10=5Le couple solution est (-5;10).
3. Déterminer l’ensemble des couples solutions de 15x+8y=5.
On soustrait membre à membre ces deux égalités :
15x+8y=5\\15\times (-5)+8\times 10=5\\15x-15\times (-5)+8y-8\times 10=5-5On réduit
15x-15\times (-5)+8y-8\times 10=0On factorise
15(x+5)+8(y-10)=0\\15(x+5)=-8(y-10)\\15 et 8 sont premiers entre eux donc d’après le théorème de Gauss, 15 divise y-10.
Donc il existe un entier relatif k tel que y-10=15k.
Donc y=15k+10
On remplace y-10 par 15k dans 15(x+5)=-8(y-10).
15(x+5)=-8\times 15k\\x+5=-8k\\x=-8k-5Les couples solutions sont de la forme (-8k-5;15k+10) avec k\in \mathbf{Z}.
On s’assure que les solutions trouvées sont bien solutions de l’équation 15x+8y=5.
15(-8k-5)+8(15k+10)=-120k-75+120k+80=5Exercice n°3
Soit l’équation 3x-4y=6
- Déterminer une solution particulière de l’équation 3x-4y=6.
2. Déterminer l’ensemble des solutions entières.
Exercice n°4
Soit l’équation 13x-23y=1
- Déterminer une solution particulière de l’équation 13x-23y=1 en utilisant l’algorithme d’Euclide.
2. Déterminer l’ensemble des solutions entières.
Exercice n°5
Soit l’équation 16x+21y=797
- a.Déterminer une solution particulière de l’équation 16x+21y=1 en utlisant l’algorithme d’Euclide.
- b .En déduire une solution particulière de l’équation 16x+21y=797.
2. Résoudre l’équation 16x+21y=797
Exercice n°6
On veut résoudre le système suivant dans \mathbf{Z}.
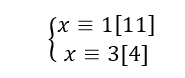
1. Montrer que résoudre ce système revient à résoudre l’équation 11u-4v=2 où u et v sont des entiers relatifs.
2. Résoudre l’équation 11u-4v=2
3. En déduire les solutions du système