logo

TS. Bac2021 espace exercice n°3

Exercice n°3 ( Amérique du nord session 2021 )

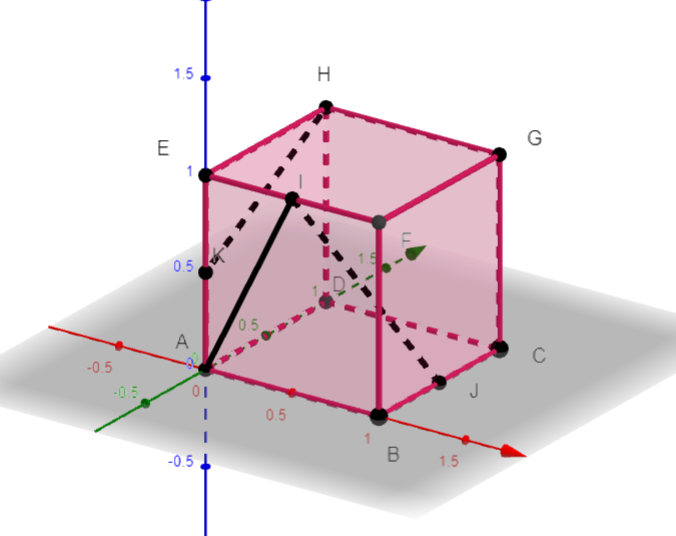
On considère le cube ABCDEFGH de côté 1. Le point I est le milieu du segment [EF], le point J est le milieu du segment [BC] et le point K est le milieu du segment [AE].

1. Les droites (AI) et (KH) sont-elles parallèles ? Justifier votre réponse.

correction

Dans la suite, on se place dans le repère orthonormé (A;\overrightarrow{AB};\overrightarrow{AD};\overrightarrow{AE})
2. a. Donner les coordonnées des points A, B, C, D, E, F et G.

Pour afficher les coordonnées du point H, par exemple, cliquer droit sur le point H de la fenêtre active Géogébra ci-dessus. Apparaît alors Point  H(0;1;1).

correction

2. b. Calculer les coordonnées des points Iet J.

Lors de leurs constructions respectives dans la fenêtre Géogébra ci-dessus, leurs coordonnées sont apparues dans la colonne Algèbre située à gauche. 

correction point I
correction point J

2. c. Montrer que les vecteurs \overrightarrow{IJ}, \overrightarrow{AE} et \overrightarrow{AC} sont coplanaires.

Lors de leurs constructions respectives dans la fenêtre Géogébra ci-dessus, leurs coordonnées sont apparues dans la colonne Algèbre située à gauche. 

correction

On considère le plan P d’équation  x+3y-2z=0 ainsi que les droites d_1 et d_2.

représentation paramétrique de d_1

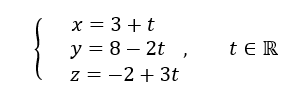
représentation paramétrique de d_2

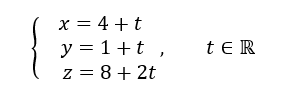
3. Les droites d_1 et d_2 sont-elles parallèles ? Justifier votre réponse. 

correction

4. Montrer que la droite d_2 est parallèle au plan P .

correction

5. Montrer que le point L(4;0;3)est le projeté orthogonal du point M(5;3;1) sur le plan P.

correction

©2020 – Math’O karé SAS

On va utiliser une démonstration par l’absurde.

On va supposer que les droites (AI) et (KH) sont parallèles.

On va montrer que c’est impossible, ce qu’on avait supposé étant faux, c’est le contraire qui est vrai c’est-à-dire que les droites (AI) et (KH) sont parallèles.

On suppose que les droites (AI) et (KH) sont parallèles.

Comme les points A;E;H sont coplanaires, I est aussi dans le plan (AEH) ce qui est impossible.

Donc les droites (AI) et (KH) ne sont pas parallèles.

Pour déterminer les coordonnées d’un point , il faut :

Partir de l’origine  A  pour se rendre au point  en se déplaçant d’abord suivant la direction du premier vecteur du repère ( ici \overrightarrow{AB}) puis suivant la direction du deuxième vecteur du repère ( ici \overrightarrow{AD}) et enfin suivant la direction du troisième vecteur du repère  ( ici \overrightarrow{AE}).

A est l’origine du repère donc A(0;0;0)

On part de  A, pour aller à B on se déplace de  1\times\overrightarrow{AB} puis de  0\times\overrightarrow{AD} et de  0\times\overrightarrow{AE} donc B(1;0;0)

On part de  A, pour aller à C on se déplace de  1\times\overrightarrow{AB} puis de  1\times\overrightarrow{AD} et de  0\times\overrightarrow{AE} donc C(1;1;0)

On part de  A, pour aller à D on se déplace de  0\times\overrightarrow{AB} puis de  1\times\overrightarrow{AD} et de  0\times\overrightarrow{AE} donc D(0;1;0)

On part de  A, pour aller à E on se déplace de  0\times\overrightarrow{AB} puis de  0\times\overrightarrow{AD} et de  1\times\overrightarrow{AE} donc E(0;0;1)

On part de  A, pour aller à F on se déplace de  1\times\overrightarrow{AB} puis de  0\times\overrightarrow{AD} et de  1\times\overrightarrow{AE} donc F(1;0;1)

On part de  A, pour aller à G on se déplace de  1\times\overrightarrow{AB} puis de  1\times\overrightarrow{AD} et de  0\times\overrightarrow{AE} donc G(1;1;1)

On part de  A, pour aller à H on se déplace de  0\times\overrightarrow{AB} puis de  1\times\overrightarrow{AD} et de  1\times\overrightarrow{AE} donc H(0;1;1)

 

 

E(0;0;1) et F(1;0;1)

Pour déterminer les coordonnées du point I milieu de [EF] : on remplace x_E par 0, y_E par 0 z_E par 1, x_F par 1, y_F par 0 z_F par 1.  dans :

 x_I=\frac{x_E+x_F}{2} ;  y_I=\frac{y_E+y_F}{2} et  z_I=\frac{z_E+z_F}{2}

 x_I=\frac{0+1}{2} ;  y_I=\frac{0+0}{2} et  z_I=\frac{1+1}{2}

 x_I=\frac{1}{2} ;  y_I=0 et  z_I=1

Donc  I(\frac{1}{2};0;1)

B(1;0;0) et C(1;1;0)

Pour déterminer les coordonnées du point J milieu de [BC] : on remplace x_B par 1, y_B par 0 z_B par 0, x_C par 1, y_C par 1 z_C par 0.  dans :

 x_J=\frac{x_B+x_C}{2} ;  y_J=\frac{y_B+y_C}{2} et  z_J=\frac{z_B+z_C}{2}

 x_J=\frac{1+1}{2} ;  y_J=\frac{0+1}{2} et  z_J=\frac{0+0}{2}

 x_J=1 ;  y_J=\frac{1}{2} et  z_J=0

Donc  J(1;\frac{1}{2};0)

On calcule les coordonnées du vecteur \overrightarrow{IJ}.

Je repère les coordonnées des points I et J.

\hspace{0.2cm}x_{I}\hspace{0.05cm}y_{I}\hspace{0.05cm}z_{I}\hspace{2.1cm}x_{J}\hspace{0.05cm}y_{J}\hspace{0.05cm}z_{J}

I(\frac{1}{2};0;1)\hspace{2cm}J(1;\frac{1}{2};0)

J’écris la formule :

\overrightarrow{IJ}(x_{J}-x_{I};y_{J}-y_{I};z_{J}-z_{I})

On prend soin de remplacer les lettres par les bons nombres. ATTENTION : quand on remplace une lettre par un nombre négatif, on le met entre parenthèses.

\overrightarrow{IJ}(1-\frac{1}{2};\frac{1}{2}-0;0-1)\\\overrightarrow{IJ}(\frac{1}{2};\frac{1}{2};-1)

On ne calcule pas les coordonnées du vecteur \overrightarrow{AE}. Comme A est l’origine du repère, le vecteur \overrightarrow{AE} a les mêmes coordonnées que le point E.

\overrightarrow{AE}(0;0;1)

On ne calcule pas les coordonnées du vecteur \overrightarrow{AC}. Comme A est l’origine du repère, le vecteur \overrightarrow{AC} a les mêmes coordonnées que le point C.

\overrightarrow{AC}(1;1;0).

Pour montrer que les vecteurs \overrightarrow{IJ} , \overrightarrow{AE} et \overrightarrow{AC} sont coplanaires, il faut montrer que l’un est une combinaison linéaire des deux autres.

En examinant les coordonnées des trois vecteurs, on voit que celles de \overrightarrow{AC} sont égales à deux fois celles de \overrightarrow{IJ} plus deux fois celles de \overrightarrow{AE}.

Ainsi \overrightarrow{AC}=2\overrightarrow{IJ}+2\overrightarrow{AE}.

Donc les vecteurs \overrightarrow{IJ} , \overrightarrow{AE} et \overrightarrow{AC} sont coplanaires.

 

La droite d_1 dont la représentation paramétrique est ci-dessous, a pour vecteur directeur le vecteur de coordonnées  (1;-2;3)

La droite d_2 dont la représentation paramétrique est ci-dessous, a pour vecteur directeur le vecteur de coordonnées  (1;1;2)

Les coordonnées  (1;-2;3) et (1;1;2) ne sont pas proportionnelles donc les vecteurs directeurs ne sont pas colinéaires donc d_1 et d_2 ne sont pas parallèles.

 

Pour montrer que la droite d_2 est parallèle au plan P, on va montrer qu’un vecteur directeur \overrightarrow{u_2} de d_2 est orthogonal à un vecteur normal \overrightarrow{n}de P.

\overrightarrow{u_2}(1;1;2) ( voir question précédente).

Comme P a pour  équation x+3y-2z=0 alors \overrightarrow{n} a pour coordonnées (1;3;-2)

On calcule ensuite \overrightarrow{u_2}.\overrightarrow{n}.

Pour calculer \overrightarrow{u_2}.\overrightarrow{n}, on remplace

x par  1 ,  y par 1 ,  z par 2.

Et

 x’ par 1 ,  y’ par 3 ,  z’ par -2.

Dans

\overrightarrow{u}.\overrightarrow{v}=xx’+yy’+zz’

 \overrightarrow{u_2}.\overrightarrow{n}=1\times 1+1\times 3+2\times (-2)\\\overrightarrow{u_2}.\overrightarrow{n}=1+3-4\\\overrightarrow{u_2}.\overrightarrow{n}=0

Donc les vecteurs \overrightarrow{u_2} et \overrightarrow{n} sont orthogonaux. Comme le vecteur \overrightarrow{n} est orthogonal au plan P.

Alors  d_2 est parallèle à P

 

Il faut montrer que le point L(4;0;3)est le projeté orthogonal du point M(5;3;1) sur le plan P.

  • Montrons d’abord que le vecteur \overrightarrow{LM} est orthogonal au plan P en montrant qu’il est colinéaire au vecteur \overrightarrow{n}(1;3;-2) vu dans la question précédente.

On calcule les coordonnées du vecteur \overrightarrow{LM}.

Je repère les coordonnées des points L et M.

\hspace{0.2cm}x_{L}\hspace{0.05cm}y_{L}\hspace{0.05cm}z_{L}\hspace{2.1cm}x_{M}\hspace{0.05cm}y_{M}\hspace{0.05cm}z_{M}

L(4;0;3)\hspace{2cm}M(5;3;1)

J’écris la formule :

\overrightarrow{LM}(x_{M}-x_{L};y_{M}-y_{L};z_{M}-z_{L})

On prend soin de remplacer les lettres par les bons nombres. ATTENTION : quand on remplace une lettre par un nombre négatif, on le met entre parenthèses.

\overrightarrow{LM}(5-4;3-0;1-3)

\overrightarrow{LM}(1;3;-2)

Comme \overrightarrow{LM} et \overrightarrow{n} sont égaux, \overrightarrow{LM} est bien orthogonal au plan P.

  • Montrons ensuite que le point  L appartient au plan P.

Montrons que les coordonnées du point L vérifient l’équation du plan P.

x_L+3y_L-2z_L+2=4+3\times 0-2\times 3+2 \\\hspace{3cm}=4+0-6+2 \\\hspace{3cm}=0

Donc le point  L appartient au plan P.

Donc le point Lest le projeté orthogonal du point M sur le plan P.

 

 

Réponse:

\overrightarrow{DC}=\overrightarrow{HG}.

Résoudre graphiquement f(x)=1

C’est une autre façon de demander de déterminer graphiquement les antécédents de 1.

Je place 1 sur l’axe des ordonnées, je trace alors la parallèle à l’axe des abscisses passant par 1 toute entière. Je repère les points d’intersection avec la courbe. Les abscisses de ces points sont les antécédents de 1.

Les antécédents sont -2 et 2.

Donc S=\{-2;2\}

Remarque : comme on demande de résoudre une équation, il faut écrire ainsi l’ensemble des solutions.