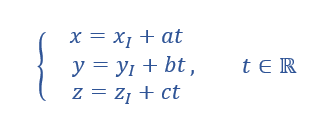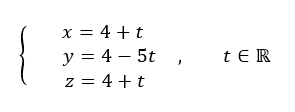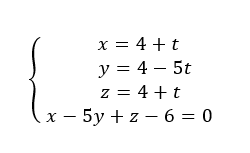logo

TS. Bac2021 espace exercice n°5

Exercice n°5 ( Asie 7 juin 2021 )

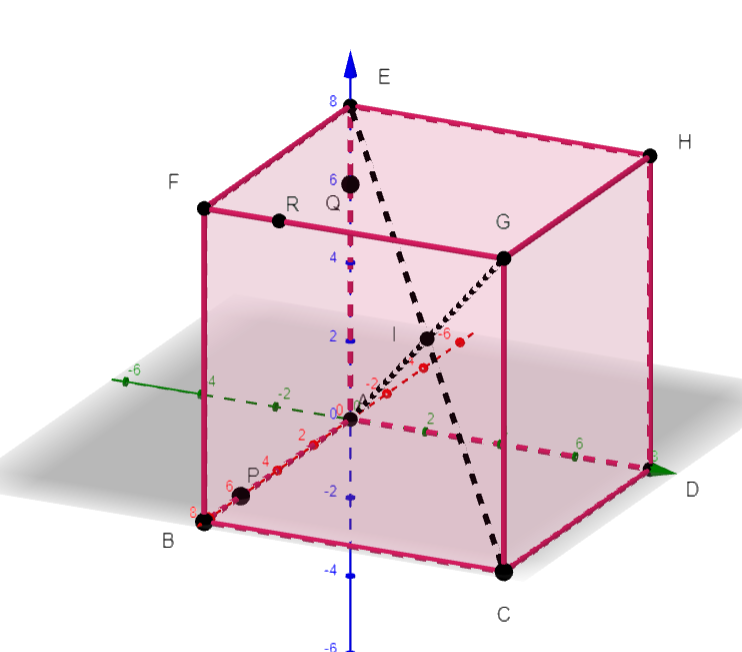
Dans l’espace, on considère le cube ABCDEFGH de côté 8 et de centre I.

P est défini par \overrightarrow{AP}=\frac{3}{4}\overrightarrow{AB} , Q est défini par \overrightarrow{AQ}=\frac{3}{4}\overrightarrow{AE} et  R est défini par \overrightarrow{FR}=\frac{1}{4}\overrightarrow{FG}.

L’espace est rapporté au repère orthonormé (A;\overrightarrow{i};\overrightarrow{j};\overrightarrow{k}) où  \overrightarrow{i}=\frac{1}{8}\overrightarrow{AB},  \overrightarrow{j}=\frac{1}{8}\overrightarrow{AD} et  \overrightarrow{k}=\frac{1}{8}\overrightarrow{AE}

Partie I
1. Dans ce repère, on admet que les coordonnées du point R sont (8;2;8).
Lire graphiquement les coordonnées des points P et Q.

Lors de la construction du point R, ses coordonnées sont apparues dans la colonne Algèbre située à gauche de l’écran  R=(8,2,8).Idem pour les points P et Q.

correction

2. Montrer que le vecteur \overrightarrow{n}(1;-5,1) est un vecteur normal au plan (PQR).

correction

3. Justifier qu’une équation cartésienne du plan (PQR) est x-5y+z-6=0.

Pour conjecturer une équation cartésienne du plan (PQR) à l’aide de la fenêtre active géogébra ci-dessus. Cliquer sur le huitième onglet en haut à partir de la gauche et sélectionner Plan passant par 3 points dans le menu déroulant. Dans le repère cliquer sur le point P puis sur le point Q et sur le point R . Dans la colonne Algèbre située à gauche, apparaît une équation cartésienne du plan   (PQR) :x-5y+z=6.

correction

Partie II
On note L le projeté orthogonal du point I sur le plan (PQR).
1. Justifier que les coordonnées du point I sont (4;4;4).

Lors de la construction du point I, ses coordonnées sont apparues dans la colonne Algèbre située à gauche de l’écran  I=(4,4,4).

correction

2. Donner une représentation paramétrique de la droite d perpendiculaire au plan (PQR)
et passant par I.

Pour conjecturer une représentation paramétrique de la droite d à l’aide de la fenêtre active géogébra ci-dessus. Cliquer sur le quatrième onglet en haut à partir de la gauche et sélectionner Orthogonale dans le menu déroulant. Dans le repère cliquer sur le point I puis sur le plan (PQR) . Dans la colonne Algèbre située à gauche, apparaît une représentation paramétrique de la droite d  :  X=(4,4,4)+\lambda (12,-60,12).

correction

3. Montrer que les coordonnées du point L sont (\frac{14}{3};\frac{2}{3};\frac{14}{3})

Pour conjecturer les coordonnées du point L à l’aide de la fenêtre active géogébra ci-dessus. Cliquer sur le deuxième onglet en haut à partir de la gauche et sélectionner Intersection dans le menu déroulant. Dans le repère cliquer sur la droite  d puis sur le plan (PQR) . Dans la colonne Algèbre située à gauche, apparaît  J=intersection(f,p)   :  (4.67,0.67,4.67).

Remarque : on peut renommer J en L.

correction

4. Calculer la distance du point I au plan (PQR).

Pour conjecturer la distance  IL à l’aide de la fenêtre active géogébra ci-dessus. Cliquer sur le onzième onglet en haut à partir de la gauche et sélectionner Distance ou longueur dans le menu déroulant. Dans le repère cliquer sur le point 0 puis sur le point H. Dans la colonne Algèbre située à gauche, apparaît la distance 3.46.

correction

©2020 – Math’O karé SAS

Pour déterminer les coordonnées d’un point, il faut :

Partir de l’origine  A  pour se rendre au point en se déplaçant d’abord suivant la direction du premier vecteur du repère ( ici \overrightarrow{i}) puis suivant la direction du deuxième vecteur du repère ( ici \overrightarrow{j}) et enfin suivant la direction du troisième vecteur du repère  ( ici \overrightarrow{k}).

On part de  A pour se rendre en P, on se déplace de  6\overrightarrow{i} puis de  0\overrightarrow{j} et de  0\overrightarrow{k}. 

Donc P(6;0;0) dans le repère  (A; \overrightarrow{i};\overrightarrow{j}; \overrightarrow{k}).

On part de A pour se rendre en Q, on se déplace de  0\overrightarrow{i} puis de  0\overrightarrow{j} et de  6\overrightarrow{k}. 

Donc Q(0;0;6) dans le repère  (A; \overrightarrow{i};\overrightarrow{j}; \overrightarrow{k}).

Pour montrer que le vecteur  \overrightarrow{n} est normal au plan (PQR), on va montrer qu’il est orthogonal aux vecteurs non colinéaires  \overrightarrow{PQ} et \overrightarrow{PR}.

On commence par calculer les coordonnées des vecteurs \overrightarrow{PQ} et \overrightarrow{PR}.

On calcule les coordonnées du vecteur \overrightarrow{PQ}.

Je repère les coordonnées des points P et Q.

\hspace{0.2cm}x_{P}\hspace{0.05cm}y_{P}\hspace{0.05cm}z_{P}\hspace{2.1cm}x_{Q}\hspace{0.05cm}y_{Q}\hspace{0.05cm}z_{Q}

P(6;0;0)\hspace{2cm}Q(0;0;6)

J’écris la formule :

\overrightarrow{PQ}(x_{Q}-x_{P};y_{Q}-y_{P};z_{Q}-z_{P})

On prend soin de remplacer les lettres par les bons nombres. ATTENTION : quand on remplace une lettre par un nombre négatif, on le met entre parenthèses.

\overrightarrow{PQ}(0-6;0-0;6-0)

\overrightarrow{PQ}(-6;0;6)

On calcule les coordonnées du vecteur \overrightarrow{PR}.

Je repère les coordonnées des points P et R.

\hspace{0.2cm}x_{P}\hspace{0.05cm}y_{P}\hspace{0.05cm}z_{P}\hspace{2.1cm}x_{R}\hspace{0.05cm}y_{R}\hspace{0.05cm}z_{R}

P(6;0;0)\hspace{2cm}R(8;2;8)

J’écris la formule :

\overrightarrow{PR}(x_{R}-x_{P};y_{R}-y_{P};z_{R}-z_{P})

On prend soin de remplacer les lettres par les bons nombres. ATTENTION : quand on remplace une lettre par un nombre négatif, on le met entre parenthèses.

\overrightarrow{PR}(8-6;2-0;8-0)

\overrightarrow{PR}(2;2;8)

Ensuite on calcule les produit scalaires  \overrightarrow{n}.\overrightarrow{PQ} et \overrightarrow{n}.\overrightarrow{PR}.

On calcule le produit scalaire  \overrightarrow{n}.\overrightarrow{PQ}.

\overrightarrow{n}(1;-5;1).

\overrightarrow{PQ}(-6;0;6).

Pour calculer  \overrightarrow{n}.\overrightarrow{PQ}, on remplace : 

 x par 1 ,  y par (-5) ,  z par 1.

 x’ par (-6) ,  y’ par 0 ,  z’ par 6, dans :

\overrightarrow{u}.\overrightarrow{v}=xx’+yy’+zz’

 \overrightarrow{n}.\overrightarrow{PQ}=1\times (-6)+(-5)\times 0+1\times 6\\\overrightarrow{n}.\overrightarrow{PQ}=-6+ 0+ 6\\\overrightarrow{n}.\overrightarrow{PQ}=0

Donc les vecteurs  \overrightarrow{n} et  \overrightarrow{PQ} sont orthogonaux.

On calcule le produit scalaire  \overrightarrow{n}.\overrightarrow{PR}.

\overrightarrow{n}(1;-5;1).

\overrightarrow{PR}(2;2;8).

Pour calculer  \overrightarrow{n}.\overrightarrow{PQ}, on remplace : 

 x par 1 ,  y par (-5) ,  z par 1.

 x’ par 2 ,  y’ par 2 ,  z’ par 8, dans :

\overrightarrow{u}.\overrightarrow{v}=xx’+yy’+zz’

 \overrightarrow{n}.\overrightarrow{PR}=1\times 2+(-5)\times 2+1\times 8\\\overrightarrow{n}.\overrightarrow{PR}=2-10+8\\\overrightarrow{n}.\overrightarrow{PR}=0

Donc les vecteurs  \overrightarrow{n} et  \overrightarrow{PR} sont orthogonaux.

Le vecteur   \overrightarrow{n} est orthogonal à   \overrightarrow{PQ} et \overrightarrow{PR}, donc il est normal au plan (PQR)

 

On veut déterminer une équation cartésienne du plan  (PQR) de vecteur normal \overrightarrow{n}.

On utilise le résultat du cours suivant : Un plan P de vecteur normal \overrightarrow{n}(a;b;c) a une équation cartésienne de la forme ax+by+cz+d=0 où d est un nombre réel.

Comme \overrightarrow{n} a pour coordonnées (1;-5;1).

On remplace a par 1 et b par (-5) et c par 1 dans l’équation  ax+by+cz+d=0.

Une équation cartésienne de (PQR) est de la forme :

1\times x+(-5)\times y+1\times z+d=0

x-5y+z+d=0

Pour déterminer d, il faut remplacer x,  y et z par les coordonnées d’un point du plan et résoudre l’équation dont d est l’inconnue.

(PQR) passe par P(6;0;0), on remplace x par 6,  y par 0 et z par 0 dans x-5y+z+d=0.

6-5\times 0+ 0+d=0

6+d=0

d=-6

Une équation cartésienne du plan  (PQR) est x-5y+z-6=0

I est le centre du cube donc c’est le milieu de [AG].

A(0;0;0) et G(8;8;8).

On remplace x_A, y_A et z_A par 0, x_G par 8, y_G par 8 et z_G par 8 dans 

x_I=\frac{x_A+x_G}{2}\hspace{2cm}y_I=\frac{y_A+y_G}{2}\hspace{2cm}z_I=\frac{z_A+z_G}{2}

x_I=\frac{0+8}{2}\hspace{2.4cm}y_I=\frac{0+8}{2}\hspace{2.4cm}z_I=\frac{0+8}{2}\\x_I=4\hspace{2.8cm}y_I=4\hspace{2.8cm}z_I=4

Donc I(4;4;4).

 

 

On veut déterminer une représentation paramétrique de la droite d perpendiculaire au plan (PQR)
et passant par I.
Pour déterminer une représentation paramétrique de la droite d, il faut un vecteur directeur et un point de cette droite.

Comme d est orthogonale au plan (PQR), alors le vecteur normal au plan  \overrightarrow{n}(1;-5;1) est un vecteur directeur de la droite d.

De plus la droite d passe par le point I(4;4;4).

On remplace x_I par 4, y_I par 4, z_I par 4 ,a par 1, b par (-5) et c par 1 dans la représentation paramétrique :

On a déterminé une représentation paramétrique de la droite d.

 

L est le projeté orthogonal du point I sur le plan (PQR). 

L\in d donc ses coordonnées vérifient le système 

L\in (PQR) donc ses coordonnées vérifient l’équation x-5y+z-6=0 

Comme L est le point d’intersection de la droite d et du plan (PQR). On résout donc le système suivant 

On remplace x,y,z en fonction de t dans la quatrième équation que l’on résout.

(4+t)-5(4-5t)+(4+t)-6=0\\4+t-20+25t+4+t-6=0\\27t-18=0\\27t=18\\t=\frac{18}{27}\\t=\frac{2}{3}

Pour trouver les valeurs de x,y,z, on remplace t par \frac{2}{3} dans les 3 premières équations.

x=4+\frac{2}{3}\\x=4\times \frac{3}{3}+\frac{2}{3}\\x= \frac{12}{3}+\frac{2}{3}\\x= \frac{14}{3}
y=4-5\times \frac{2}{3}\\y=4-\frac{10}{3}\\y=4\times \frac{3}{3}-\frac{10}{3}\\y= \frac{12}{3}-\frac{10}{3}\\y= \frac{2}{3}
z=4+\frac{2}{3}\\z=4\times \frac{3}{3}+\frac{2}{3}\\z= \frac{12}{3}+\frac{2}{3}\\z= \frac{14}{3}

Donc L a pour coordonnées (\frac{14}{3};\frac{2}{3};\frac{14}{3}).

 

 

Puisque L est le projeté orthogonal de I sur le plan (PQR) , la distance de I à ce plan
est la distance IL.

Je repère les coordonnées des points I et L.

\hspace{0.4cm}x_{I}\hspace{0.05cm}y_{I}\hspace{0.05cm}z_{I}\hspace{2.4cm}x_{L}\hspace{0.05cm}y_{L}\hspace{0.05cm}z_{L}

I(4;-4;4)\hspace{2cm}L(\frac{14}{3};\frac{2}{3};\frac{14}{3})

J’écris la formule :

IL=\sqrt{(x_{L}-x_{I})^2+(y_{L}-y_{I})^2;(z_{L}-z_{I})^2}

On prend soin de remplacer les lettres par les bons nombres. ATTENTION : quand on remplace une lettre par un nombre négatif, on le met entre parenthèses.

IL=\sqrt{(\frac{14}{3}-4)^2+(\frac{2}{3}-4)^2+(\frac{14}{3}-4)^2}\\IL=\sqrt{(\frac{14}{3}-\frac{12}{3})^2+(\frac{2}{3}-\frac{12}{3})^2+(\frac{14}{3}-\frac{12}{3})^2}\\IL=\sqrt{(\frac{2}{3})^2+(-\frac{10}{3})^2+(\frac{2}{3})^2}\\IL=\sqrt{\frac{4}{9}+\frac{100}{9}+\frac{4}{9}}\\IL=\sqrt{\frac{108}{9}}\\IL=\sqrt{12}\\IL=2\sqrt{3}

Donc la distance de I au plan (PQR) vaut 2\sqrt{3}

 

Réponse:

\overrightarrow{DC}=\overrightarrow{HG}.

Résoudre graphiquement f(x)=1

C’est une autre façon de demander de déterminer graphiquement les antécédents de 1.

Je place 1 sur l’axe des ordonnées, je trace alors la parallèle à l’axe des abscisses passant par 1 toute entière. Je repère les points d’intersection avec la courbe. Les abscisses de ces points sont les antécédents de 1.

Les antécédents sont -2 et 2.

Donc S=\{-2;2\}

Remarque : comme on demande de résoudre une équation, il faut écrire ainsi l’ensemble des solutions.