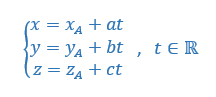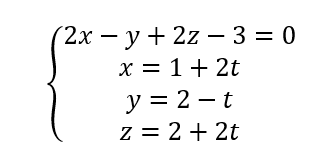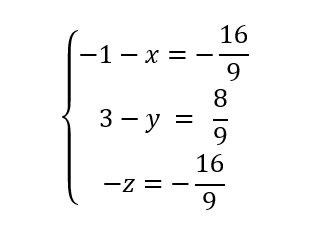Dans l’espace rapporté à un repère orthonormé (O,\overrightarrow{i}, \overrightarrow{j}, \overrightarrow{k}). On considère :
• le point A de coordonnées (-1,1,3)
• la droite D dont une représentation paramétrique est :
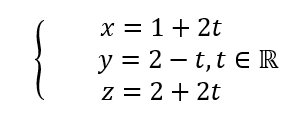
On admet que le point A n’appartient pas à la droite D.
1. a. Donner les coordonnées d’un vecteur directeur \overrightarrow{u} de la droite D.
b. Montrer que le point B(-1,3,0) appartient à la droite D.
c. Calculer le produit scalaire \overrightarrow{AB}.\overrightarrow{u}.
2. On note P le plan passant par le point A et orthogonal à la droite D, et on appelle H le point d’intersection du plan P et de la droite D. Ainsi, H est le projeté orthogonal de A sur la droite D.
a. Montrer que le plan P admet pour équation cartésienne : 2x-y+2z-3=0.
b. En déduire que le point H a pour coordonnées (\frac{7}{9},\frac{19}{9},\frac{16}{9}).
c. Calculer la longueur AH. On donnera une valeur exacte.
3. Dans cette question, on se propose de retrouver les coordonnées du point H, projeté orthogonal du point A sur la droite D, par une autre méthode.
On rappelle que le point B(-1,3,0) appartient à la droite D et que le vecteur \overrightarrow{u} est un vecteur directeur de la droite D.
a. Justifier qu’il existe un nombre réel k tel que \overrightarrow{HB}=k\overrightarrow{u}.
b. Montrer que k=\frac{\overrightarrow{AB}.\overrightarrow{u}}{||\overrightarrow{u}||^2}.
c. Calculer la valeur du nombre réel k et retrouver les coordonnées du point H.
4. On considère un point C appartenant au plan P tel que le volume du tétraèdre ABCH soit égal à \frac{8}{9}.
Calculer l’aire du triangle ACH.
On rappelle que le volume d’un tétraèdre est donné par : V=\frac{1}{3}\times b \times h où b désigne l’aire d’une base et h la hauteur relative à cette base.