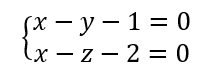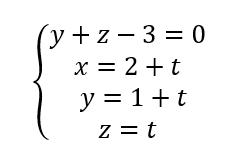logo

T. bac2022 espace exo n°3 (Centres étrangers 17 mai 2022)

L’espace est muni d’un repère orthonormé (O,\overrightarrow{i}, \overrightarrow{j}, \overrightarrow{k}).

On considère les points A(5;0;-1) , B(1;4;-1), C(5;0;-1), D(5;4;3) et E(10;9;8).

On les a placés ci-dessous dans le repère de la fenêtre active Géogébra.

1. a. Soit R le milieu du segment [AB].
Calculer les coordonnées du point R ainsi que les coordonnées du vecteur \overrightarrow{AB}.

On peut conjecturer les résultats à l’aide de Géogébra.

  1. Pour placer le point R : 
  • Cliquer sur le deuxième onglet en partant de la gauche et sélectionner Milieu ou centre dans le menu déroulant.
  • Dans le repère, cliquer sur les points A et B.
  • Le point F apparaît, ses coordonnées sont (3,2,-1). Le renommer  avec la lettre R en cliquant droit dessus et en sélectionnant Renommer dans le menu déroulant.

2. Pour construire le vecteur  \overrightarrow{AB}: 

  • Cliquer sur le troisième onglet en partant de la gauche et sélectionner vecteur dans le menu déroulant.
  • Dans le repère, cliquer sur les points A et B.
  • Dans la colonne algèbre à gauche, le vecteur  \overrightarrow{AB} apparaît, ses coordonnées sont (-4,4,0).
correction

b. Soit P_1 le plan passant par le point R et dont \overrightarrow{AB} est un vecteur normal.
Démontrer qu’une équation cartésienne du plan P_1 est : x-y-1=0.

On aurait pu conjecturer une équation cartésienne à l’aide de Géogébra.

Pour construire le plan P_1 : 

Saisir dans la colonne Algèbre située à gauche PlanOrthogonal(R,u)

Une équation de P_1 apparaît, -x+y=-1.

correction

c. Démontrer que le point E appartient au plan P_1 et que EA=EB.

On peut conjecturer les distances EA et EB à l’aide de Géogébra.

  • Cliquer sur le onzième onglet en partant de la gauche et sélectionner Distance ou Longueur dans le menu déroulant.
  • Dans le repère, cliquer sur les points E et A.
  • Dans la colonne algèbre à gauche, on lit EA=13.67. 

De la même façon, on obtient EB=13.67

correction

2. On considère le plan P_2 d’équation cartésienne x-z-2=0.
a. Justifier que les plans P_1 et P_2 sont sécants.

On peut tracer le plan P_2 à l’aide de Géogébra.

Dans la colonne algèbre à gauche, saisir x-z-2=0. 

correction

b. On note \Delta la droite d’intersection de P_1 et P_2.
Démontrer qu’une représentation paramétrique de la droite \Delta est :

correction

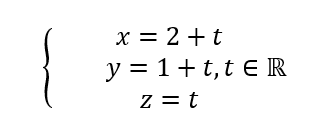
3. On considère le plan P_3 d’équation cartésienne y+z-3=0. Justifier que la droite \Delta est sécante au plan P_3 en un point \Omega dont on déterminera les coordonnées.

correction

Si S et T sont deux points distincts de l’espace, on rappelle que l’ensemble des points M de l’espace
tels que MS=MTest un plan, appelé plan médiateur du segment [ST]. On admet que les plans P_1,
P_2 et P_3 sont les plans médiateurs respectifs des segments [AB], [AC] et [AD].
4. a. Justifier que \Omega A=\Omega B=\Omega C=\Omega D.

correction

b. En déduire que les points A,B,C et D appartiennent à une même sphère dont on précisera le centre et le rayon.

correction

©2020 – Math’O karé SAS

Soit R le milieu du segment [AB].
On veut calculer les coordonnées du point R.

A(5;0;-1) et B(1;4;-1).

On remplace x_A par 5 , y_A par 0 et z_A par (-1), x_B par 1, y_B par 4 et z_B par (-1) dans 

x_I=\frac{x_A+x_G}{2}\hspace{2cm}y_I=\frac{y_A+y_G}{2}\hspace{2cm}z_I=\frac{z_A+z_G}{2}

x_I=\frac{5+1}{2}\hspace{2.4cm}y_I=\frac{0+4}{2}\hspace{2.4cm}z_I=\frac{(-1)+(-1)}{2}\\x_I=3\hspace{2.8cm}y_I=2\hspace{2.8cm}z_I=-1

Donc I(3;2;-1).

On veut calculer les coordonnées du vecteur \overrightarrow{AB}.

Je repère les coordonnées des points A et B.

\hspace{0.5cm}x_{A}\hspace{0.05cm}y_{A}\hspace{0.05cm}z_{A}\hspace{2.1cm}x_{B}\hspace{0.05cm}y_{B}\hspace{0.05cm}z_{B}

A(5;0;-1)\hspace{2cm}B(1;4;-1)

J’écris la formule :

\overrightarrow{AB}(x_{B}-x_{A};y_{B}-y_{A};z_{B}-z_{A})

On prend soin de remplacer les lettres par les bons nombres. ATTENTION : quand on remplace une lettre par un nombre négatif, on le met entre parenthèses.

\overrightarrow{AB}(1-5;4-0;(-1)-(-1))

\overrightarrow{AB}(-4;4;0)

Soit P_1 le plan passant par le point R et dont \overrightarrow{AB} est un vecteur normal.
On veut démontrer qu’une équation cartésienne du plan P_1 est : x-y-1=0.

P_1 est le plan passant par le point R et de vecteur normal \overrightarrow{AB}(-4,4,0).

On utilise le résultat du cours suivant : Un plan P de vecteur normal \overrightarrow{n}(a;b;c) a une équation cartésienne de la forme ax+by+cz+d=0 où d est un nombre réel.

On remplace a par (-4) et b par 4 et c par 0 dans l’équation  ax+by+cz+d=0.

Une équation cartésienne de P_1 est de la forme :

(-4)\times x+4y+0\times z+d=0

-4x+4y+d=0

Pour déterminer d, il faut remplacer x,  y et z par les coordonnées d’un point du plan et résoudre l’équation dont d est l’inconnue.

P_1 passe par R(3;2;-1), on remplace x par 3,  y par 2 et z par (-1) dans -4x+4y+d=0.

-4\times 3+4\times 2+d=0

-12+8+d=0

-4+d=0

d=4

Une équation cartésienne du plan est P_1 est -4x+4y+4=0.

Si on divise l’équation précédente par -4 de chaque côté :

\frac{-4x+4y+4}{-4}=\frac{0}{-4}

On obtient une nouvelle équation cartésienne du plan :

x-y-1=0.

 

On veut démontrer que le point E appartient au plan P_1.

Pour cela on montre que les coordonnées de E(10;9;8) vérifient l’équation cartésienne de P_1 précédente : x-y-1=0.

On remplace x_E par 10 , y_E par 9 , z_E par 10 dans x-y-1, on calcule et on trouve 0.

10-9-1=0 donc E \in P_1.

On veut montrer que EA=EB.

Calcul de la distanceEA

E(10;9;8)\\A(5;0;-1)

Pour calculer la distance EA, on remplace x_E par 10 , y_E par 9 , z_E par 8 , x_A par 5 , y_A par 0 et z_A par (-1) dans la formule

EA=\sqrt{(x_A-x_E)^2+(y_A-y_E)^2+(z_A-z_E)^2}

EA=\sqrt{(5-10)^2+(0-9)^2+((-1)-8)^2}

On effectue ce qu’il y a entre parenthèses 

EA=\sqrt{(-5)^2+(-9)^2+(-9)^2}

On effectue les puissances

EA=\sqrt{25+81+81}

On ajoute 

EA=\sqrt{187}

Calcul de la distance EB

E(10;9;8)\\B(1;4;-1)

Pour calculer la distance EB, on remplace x_E par 10 , y_E par 9 , z_E par 8 , x_B par 1 , y_B par 4 et z_B par (-1) dans la formule

EB=\sqrt{(x_B-x_E)^2+(y_B-y_E)^2+(z_B-z_E)^2}

EB=\sqrt{(1-10)^2+(4-9)^2+((-1)-8)^2}

On effectue ce qu’il y a entre parenthèses 

EB=\sqrt{(-9)^2+(-5)^2+(-9)^2}

On effectue les puissances

EB=\sqrt{81+25+81}

On ajoute 

EB=\sqrt{187}

Donc EA=EB.

 

On considère le plan P_2 d’équation cartésienne x-z-2=0.
On va justifier que les plans P_1 et P_2 sont sécants en montrant qu’ils ne sont pas parallèles.

Un vecteur normal à P_1 est \overrightarrow{AB}(-4;4;0).

On utilise le résultat du cours suivant : Un plan P de vecteur normal \overrightarrow{n}(a;b;c) a une équation cartésienne de la forme ax+by+cz+d=0 où d est un nombre réel.

P_2 a pour équation cartésienne x-z-2=0.

Donc un vecteur normal à P_2 est \overrightarrow{u}(1;0;-1).

Les vecteurs \overrightarrow{AB}(-4;4;0) et \overrightarrow{u}(1;0;-1) ne sont pas colinéaires car leurs coordonnées ne sont pas proportionnelles.

Donc les plans P_1 et P_2 ne sont pas parallèles, ils sont donc sécants.

 

On note \Delta la droite d’intersection de P_1 et P_2.
On veut démontrer qu’une représentation paramétrique de la droite \Delta est :

Le plan P_1 a pour équation cartésienne x-y-1=0 et le plan P_2 a pour équation cartésienne x-z-2=0.
M(x,y,z)\in P_1\cap P_2 si les coordonnées vérifient le système :

Comme il y a deux équations à trois inconnues, il faudra en exprimer deux en fonction de la troisième. L’énoncé suggère d’exprimer x et y en fonction de z.

De x-z-2=0, on obtient x=2+z.

De x-y-1=0, on obtient y=x-1=(2+z)-1=1+z.

Si on pose z=t, on obtient la représentation paramétrique de la droite \Delta:

On considère le plan P_3 d’équation cartésienne y+z-3=0.

On veut justifier que la droite \Delta est sécante au plan P_3.

Comme la représentation paramétrique de \Delta est 

Le vecteur \overrightarrow{u} de coordonnées (1;1;1) est un vecteur directeur de  \Delta.

Comme le plan P_3 a pour équation cartésienne y+z-3=0.

Le vecteur \overrightarrow{v} de coordonnées (0;1;1) est un vecteur normal de  P_3.

On calcule le produit scalaire \overrightarrow{u}.\overrightarrow{v}. 

\overrightarrow{u}.\overrightarrow{v}=1\times 0+1\times 1+1\times 1=2, Comme le produit scalaire n’est pas nul, \overrightarrow{u} et \overrightarrow{v} ne sont pas orthogonaux donc la droite \Delta n’est pas parallèle au plan P_3 donc \Delta est sécante au plan P_3.

On veut déterminer les coordonnées de \Omega.

\Omega est le point d’intersection du plan P_3 et de la droite \Delta. 

Ses coordonnées inconnues notées (x,y,z) vérifient les équations du plan P_3 et de la droite \Delta :

On remplace x,y,z en fonction de t dans la première équation que l’on résout.

1+t+t-3=0\\2t-2=0\\2t=2\\t=\frac{2}{2}\\t=1

Pour trouver les valeurs de x,y,z, on remplace t par 1 dans les 3 dernières équations.

x=2+1\\x=3
y=1+1\\y=2
z=1

Donc le point \Omega a pour coordonnées (3;2;1).

 

On veut calculer la longueur \Omega A.

\Omega(3;2;1)\\A(5;0;-1)

Pour calculer la distance \Omega A, on remplace x_\Omega par 3 , y_\Omega par 2 , z_\Omega par 1 , x_A par 5 , y_A par 0 et z_A par (-1) dans la formule

\Omega A=\sqrt{(x_A-x_\Omega )^2+(y_A-y_\Omega )^2+(z_A-z_\Omega )^2}

\Omega A=\sqrt{(5-3)^2+(0-2)^2+((-1)-1)^2}

On effectue ce qu’il y a entre parenthèses 

\Omega A=\sqrt{2^2+(-2)^2+(-2)^2}

On effectue les puissances

\Omega A=\sqrt{4+4+4}

On ajoute 

\Omega A=\sqrt{12}\\\Omega A=2\sqrt{3}

On veut calculer la longueur \Omega B.

\Omega(3;2;1)\\B(1;4;-1)

Pour calculer la distance \Omega B, on remplace x_\Omega par 3 , y_\Omega par 2 , z_\Omega par 1 , x_B par 1 , y_B par 4 et z_B par (-1) dans la formule

\Omega B=\sqrt{(x_B-x_\Omega )^2+(y_B-y_\Omega )^2+(z_B-z_\Omega )^2}

\Omega B=\sqrt{(1-3)^2+(4-2)^2+((-1)-1)^2}

On effectue ce qu’il y a entre parenthèses 

\Omega B=\sqrt{(-2)^2+2^2+(-2)^2}

On effectue les puissances

\Omega B=\sqrt{4+4+4}

On ajoute 

\Omega B=\sqrt{12}\\\Omega B=2\sqrt{3}

On veut calculer la longueur \Omega C.

\Omega(3;2;1)\\C(1;0;3)

Pour calculer la distance \Omega C, on remplace x_\Omega par 3 , y_\Omega par 2 , z_\Omega par 1 , x_C par 1 , y_C par 0 et z_C par 3 dans la formule

\Omega C=\sqrt{(x_C-x_\Omega )^2+(y_C-y_\Omega )^2+(z_C-z_\Omega )^2}

\Omega C=\sqrt{(1-3)^2+(0-2)^2+(3-1)^2}

On effectue ce qu’il y a entre parenthèses 

\Omega C=\sqrt{(-2)^2+(-2)^2+2^2}

On effectue les puissances

\Omega C=\sqrt{4+4+4}

On ajoute 

\Omega C=\sqrt{12}\\\Omega C=2\sqrt{3}

On veut calculer la longueur \Omega D.

\Omega(3;2;1)\\D(5;4;3)

Pour calculer la distance \Omega D, on remplace x_\Omega par 3 , y_\Omega par 2 , z_\Omega par 1 , x_D par 5 , y_D par 4 et z_D par 3 dans la formule

\Omega D=\sqrt{(x_D-x_\Omega )^2+(y_D-y_\Omega )^2+(z_D-z_\Omega )^2}

\Omega D=\sqrt{(5-3)^2+(4-2)^2+(3-1)^2}

On effectue ce qu’il y a entre parenthèses 

\Omega D=\sqrt{2^2+2^2+2^2}

On effectue les puissances

\Omega D=\sqrt{4+4+4}

On ajoute 

\Omega D=\sqrt{12}\\\Omega D=2\sqrt{3}

Les quatre distances sont égales à 2\sqrt{3}, donc :

\Omega A=\Omega B=\Omega C=\Omega D.

 

Comme \Omega A=\Omega B=\Omega C=\Omega D=2\sqrt{3}.

Les quatre points A,B,C,D sont situés à la distance 2\sqrt{3} du point \Omega .

Donc les quatre points A,B,C,D sont situés sur une sphère de rayon 2\sqrt{3} et de centre \Omega .

Réponse:

\overrightarrow{DC}=\overrightarrow{HG}.

Résoudre graphiquement f(x)=1

C’est une autre façon de demander de déterminer graphiquement les antécédents de 1.

Je place 1 sur l’axe des ordonnées, je trace alors la parallèle à l’axe des abscisses passant par 1 toute entière. Je repère les points d’intersection avec la courbe. Les abscisses de ces points sont les antécédents de 1.

Les antécédents sont -2 et 2.

Donc S=\{-2;2\}

Remarque : comme on demande de résoudre une équation, il faut écrire ainsi l’ensemble des solutions.