2. vecteurs / vecteurs égaux

Géométrie, Niveau seconde, Vecteurs

Activité d’approche

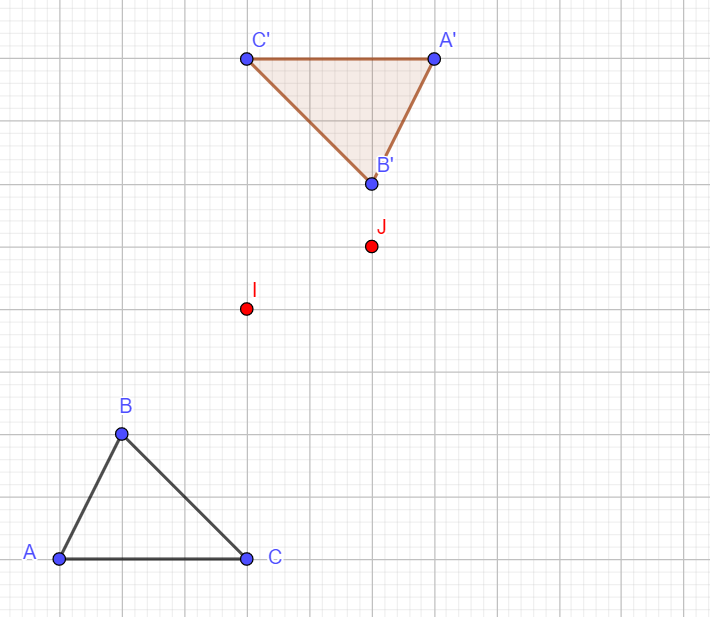
$ABC$ est un triangle quelconque.

$I$ et $J$ sont deux points du plan.

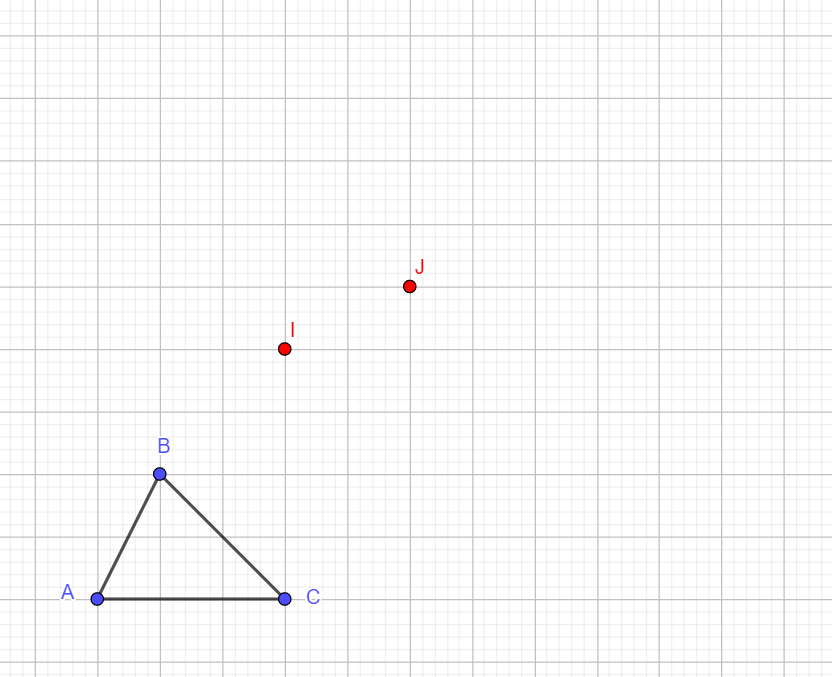
Construire le triangle $A’B’C’$ , symétrique du triangle $ABC$ par la symétrie centrale $s_{I}$ de centre $I$ .

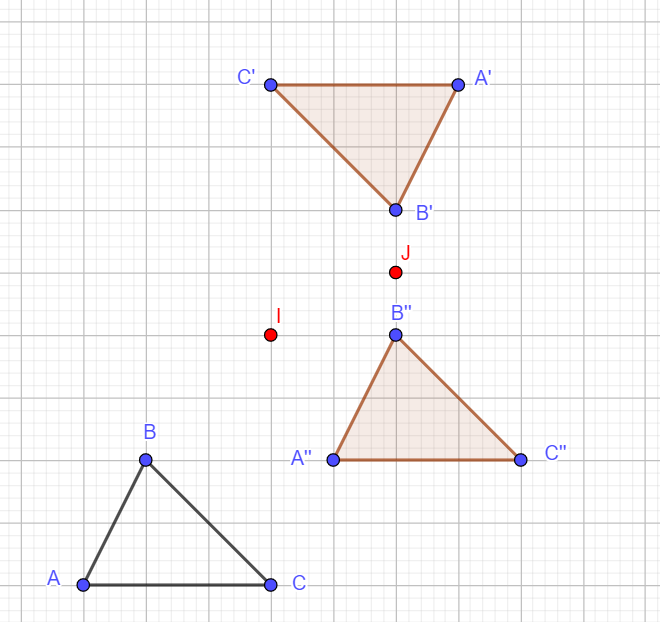
2. Construire le triangle $A"B"C"$ , le symétrique du triangle $A’B’C’$ par la symétrie centrale $s_{J}$ de centre $J$ .

3. Compléter les pointillés : Pour obtenir le point $A"$ , je pars du point $A$ , je me déplace suivant la direction de la droite $(\dots)$ dans le sens du point … vers le point … et d’une distance égale à …

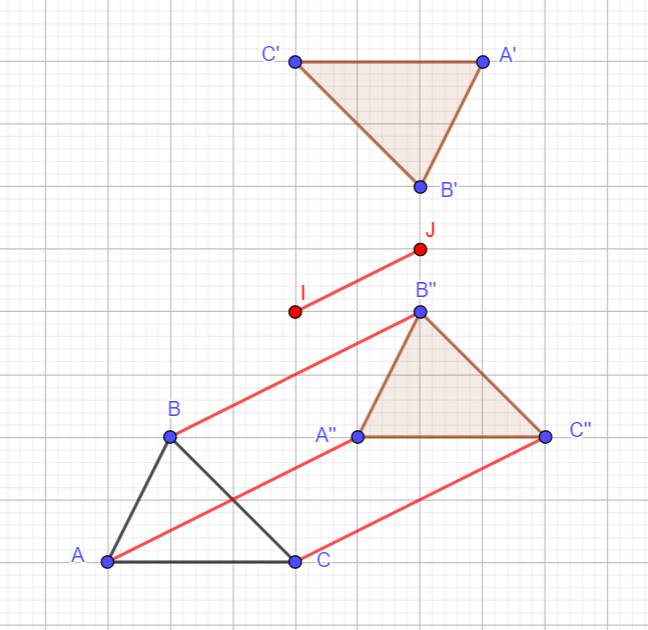
4. Synthèse : On admet qu’on obtient $B"$ et $C"$ à partir $B$ et $C$ de la même façon.

Nous dirons que $A$ , $B$ et $C$ se transforment en $A"$ , $B"$ et $C"$ par la translation de vecteur $2\overrightarrow{IJ}$ qu’on notera $t_{2\overrightarrow{IJ}}$ .

Notion de vecteur

Définition

A la translation qui transforme $M$ en $M’$ , on associe le vecteur noté $\overrightarrow{MM’}$ .

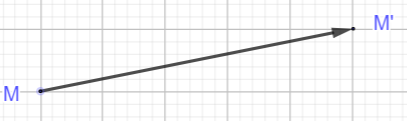
Le vecteur $\overrightarrow{MM’}$ a pour direction , la direction de la droite $(MM’)$ .

Le vecteur $\overrightarrow{MM’}$ a pour sens , le sens de $M$ vers $M’$ .

Le vecteur $\overrightarrow{MM’}$ a pour longueur ( on dit plutôt norme que l’on note $\left\|\overrightarrow{MM’}\right\|$ ) , la longueur $MM’$ .

Exercice n°1

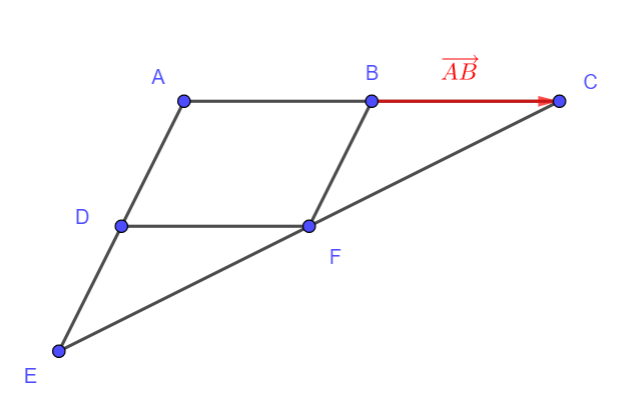
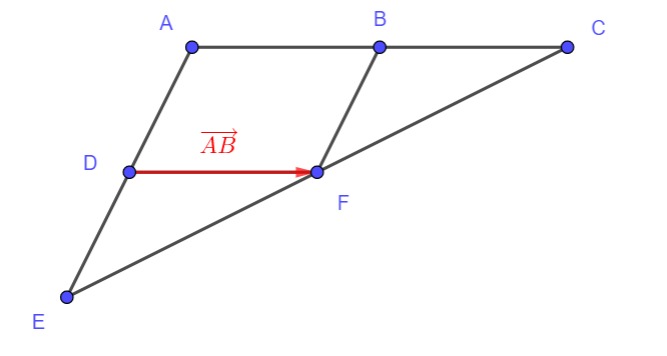
$ABFD$ est un parallélogramme.

$B$ est le milieu de $[AC]$ .

$D$ est le milieu de $[AE]$ .

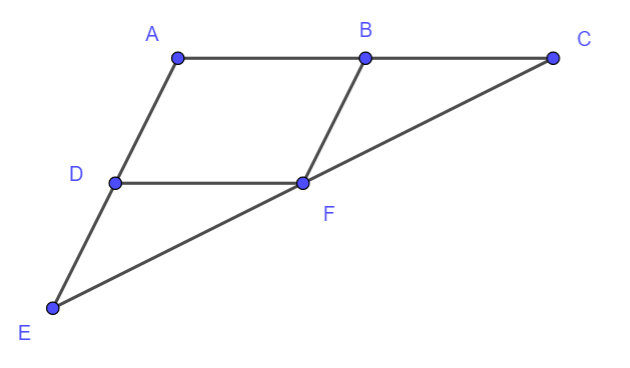
Quelle est l’image de $B$ par la translation de vecteur $\overrightarrow{AB}$ ?

2. Quelle est l’image de $D$ par la translation de vecteur $\overrightarrow{AB}$ ?

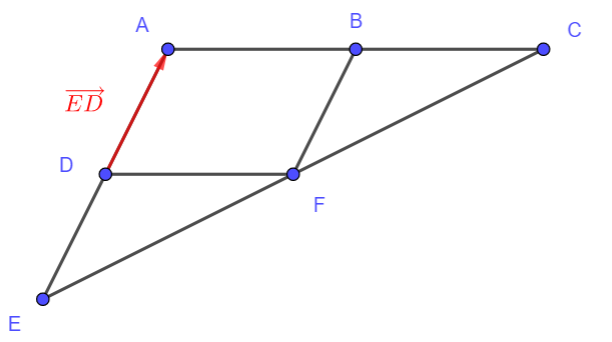
3. Compléter les pointillés $t_{\overrightarrow{ED}}(D)=…$

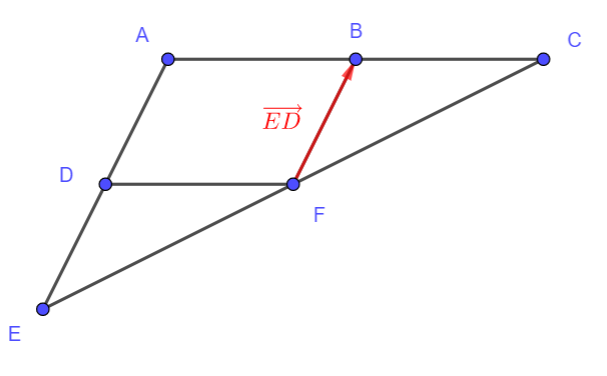
4. Compléter les pointillés $t_{\overrightarrow{ED}}(F)=…$

Vecteurs égaux

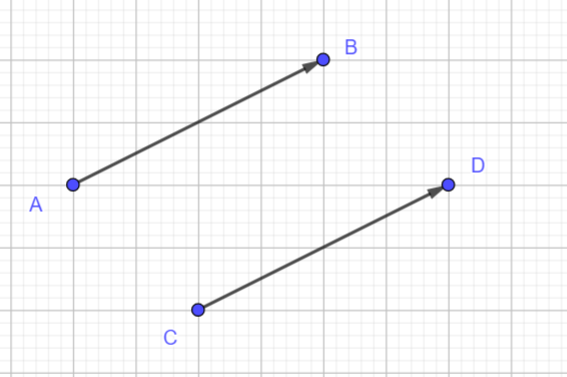
Voici 4 caractérisations de l’égalité vectorielle $\overrightarrow{AB}=\overrightarrow{CD}$

Caractérisation n°1:

D est l’image de C par la translation de vecteur $\overrightarrow{AB}$

Caratérisation n°2:

ABDC est un parallélogramme

Caractérisation n°3 :

$[AD]$ et $[BC]$ ont même milieu.

Caractérisation n°4:

$(AB)$ et $(CD)$ sont parallèles.

On va de $A$ vers $B$ comme on va de $C$ vers $D$ .

AB=CD

Exercice n°2

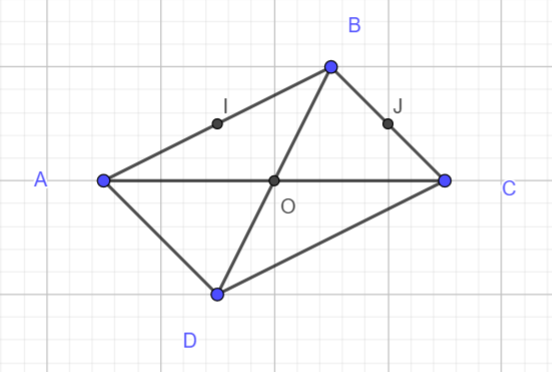
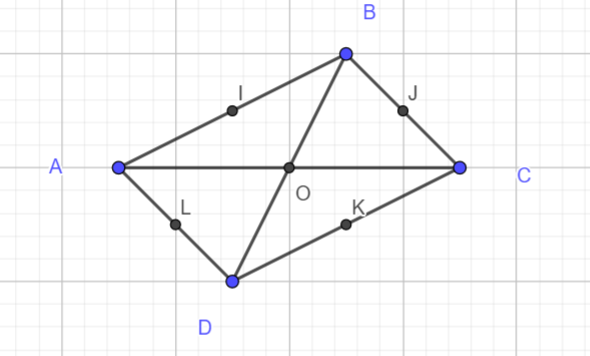
$ABCD$ est un parallélogramme. Ses diagonales $[AC]$ et $[BD]$ se coupent en O.

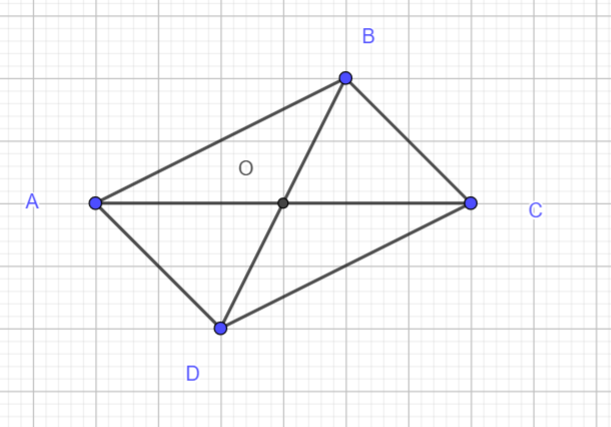
Citer un vecteur égal au vecteur $\overrightarrow{AB}$ .

2. Citer un vecteur égal au vecteur $\overrightarrow{AD}$ .

3.a. Placer $I$ et $J$ les milieux respectifs des segments $[AB]$ et $[BC]$

3.b. Citer deux vecteurs égaux au vecteur $\overrightarrow{IJ}$ .

4.a. Placer $K$ et $L$ les milieux respectifs des segments $[CD]$ et $[DA]$

4.b. Citer deux vecteurs égaux au vecteur $\overrightarrow{LK}$ .

5. Démontrer que $IJKL$ est un parallélogramme.

Méthode : placer un point défini par une égalité vectorielle

Méthode

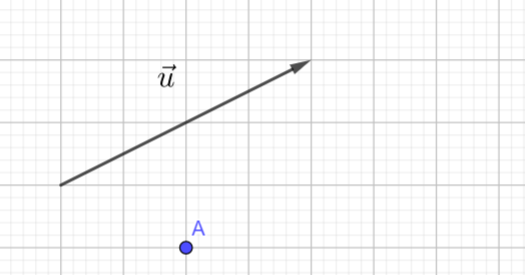
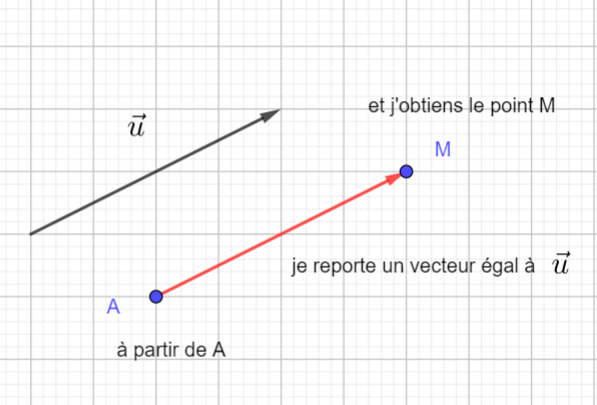
pour placer un point $M$ défini par une égalité vectorielle du type $\overrightarrow{AM}=\vec{u}$ .

A partir du point $A$ , je construis un vecteur égal au vecteur $\vec{u}$ . J’obtiens alors le point $M$ .

Exercice n°3

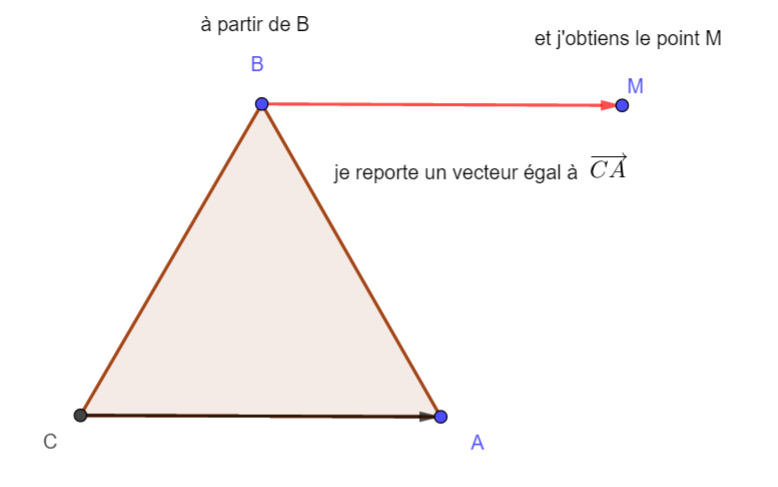
$ABC$ est un triangle équilatéral.

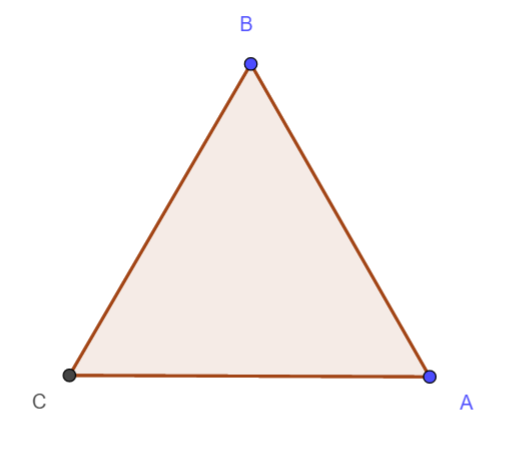
Placer le point $M$ tel que $\overrightarrow{BM}=\overrightarrow{CA}$

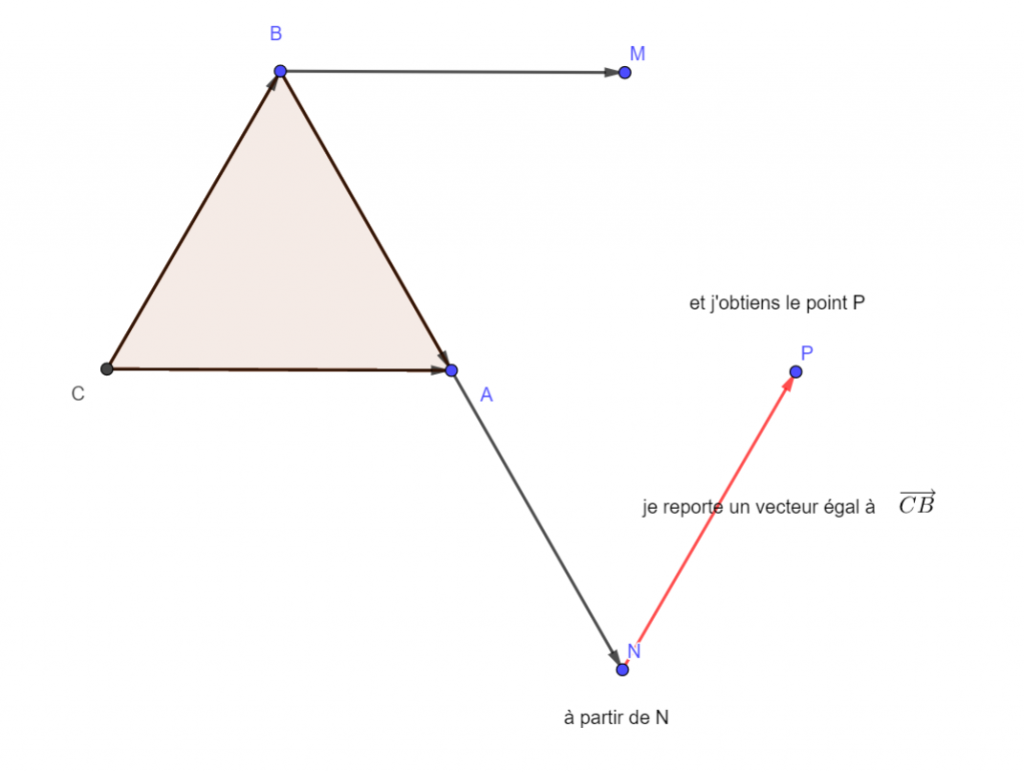
2. Placer le point $N$ tel que $\overrightarrow{AN}=\overrightarrow{BA}$

3. Placer le point $P$ tel que $\overrightarrow{NP}=\overrightarrow{CB}$

Coordonnées d’un vecteur

définition

Soit $(0, \vec{i},\vec{j})$ un repère orthonormé du plan

On dit que $M$ a pour coordonnées $x$ et $y$ , on note $M(x;y)$ si $\overrightarrow{OM}=x\vec{i}+y\vec{j}$ .

De plus si $\vec{u}=x\vec{i}+y\vec{j}$ alors $\vec{u}$ a pour coordonnées $x$ et $y$ , on note $\vec{u}(x;y)$ .

Exemple n°1

Pour déterminer graphiquement les coordonnées du vecteur $\overrightarrow{OA}$ .

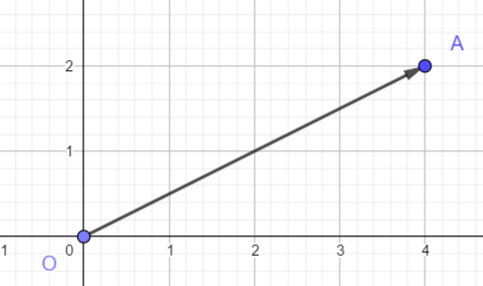
Je veux aller de O vers A, je me déplace horizontalement vers la droite de 4 graduations à partir du point O.

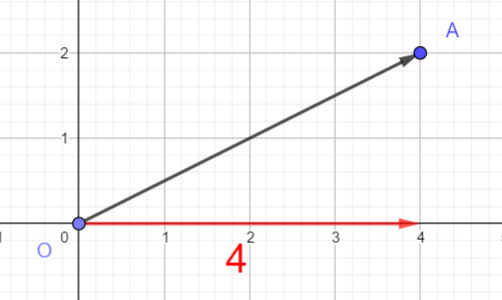
Puis je me déplace vers le haut de 2 graduations et j’arrive au point A.

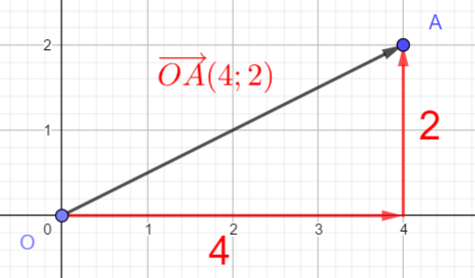
Exemple n°2

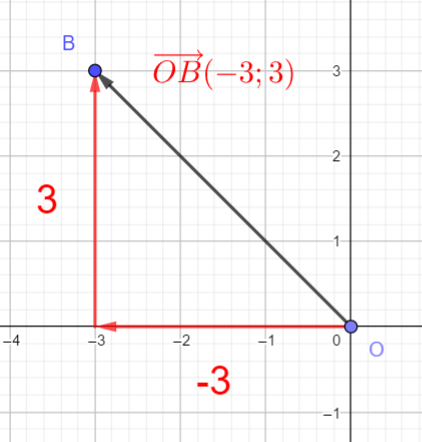
Pour déterminer graphiquement les coordonnées du vecteur $\overrightarrow{OB}$ .

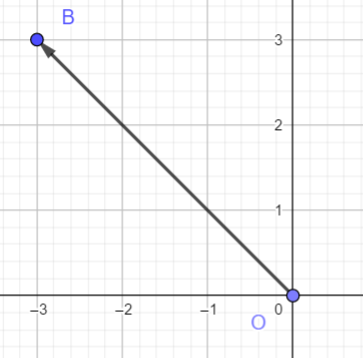
Je veux aller de O vers B, je me déplace horizontalement vers la gauche de 3 graduations à partir du point O.

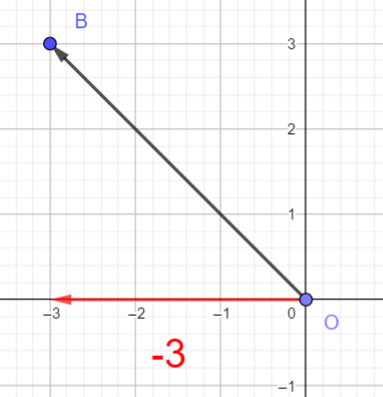
Puis je me déplace vers le haut de 3 graduations et j’arrive au point B.

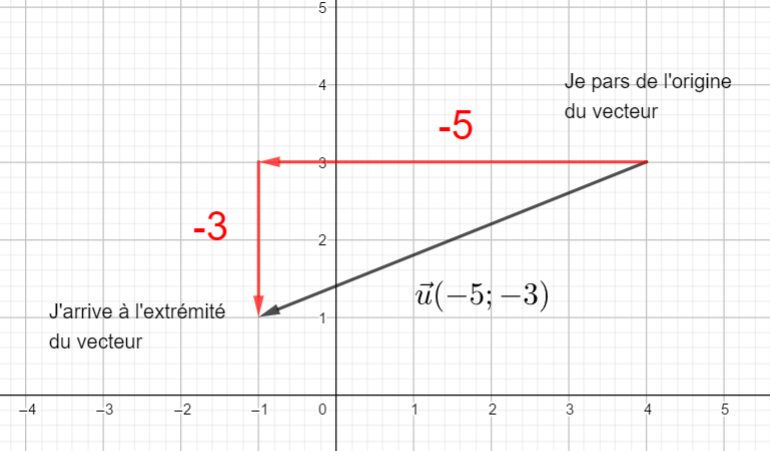
Exemple n°3

Pour déterminer graphiquement les coordonnées du vecteur $\vec{u}$ .

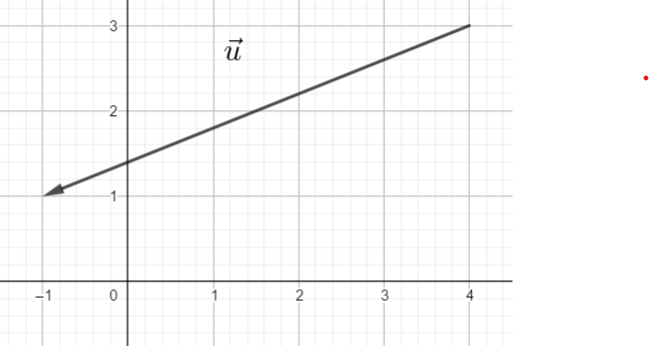
Je veux aller de l’origine du vecteur $\vec{u}$ jusqu’à l’extrémité de $\vec{u}$ , je me déplace horizontalement vers la gauche de 5 graduations à partir du point O.

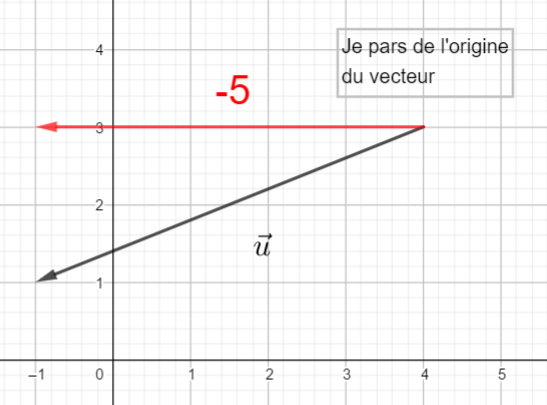
Puis je me déplace vers le bas de 2 graduations et j’arrive à l’extrémité de $\vec{u}$ .

vecteurs égaux

Deux vecteurs sont égaux si leurs coordonnées sont égales.

coordonnées d’un vecteur d’origine A et d’extrémité B

Propriété : Si $A(x_{A},y_{A})$ et $B(x_{B},y_{B})$ alors $\overrightarrow{AB}(x_{B}-x_{A},y_{B}-y_{A})$

Exercice n°4

Soient les points $A(-1;0), B(0;3), C(5;2), D(4;-1)$

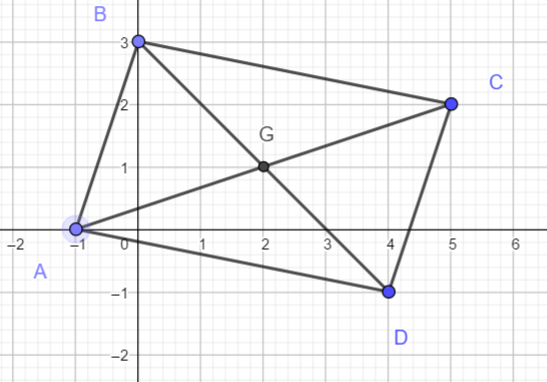
Calculer les coordonnées des vecteurs $\overrightarrow{AB}$ et $\overrightarrow{DC}$ . Que constatez-vous ? Etait-ce prévisible ?

2. Calculer les coordonnées des vecteurs $\overrightarrow{AD}$ et $\overrightarrow{BC}$ . Que constatez-vous ? Etait-ce prévisible ?

3a. Calculer les coordonnées de $G$ milieu de $[BD]$ .

3b. Calculer les coordonnées des vecteurs $\overrightarrow{AG}$ et $\overrightarrow{GC}$ . Que constatez-vous ? Etait-ce prévisible ?

Exercice n°5

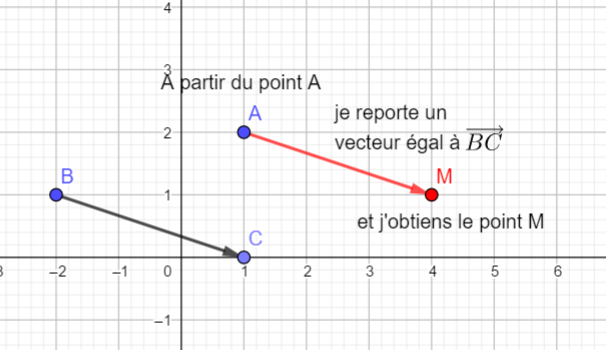
Soient les points $A(1;2), B(-2;1), C(1;0)$

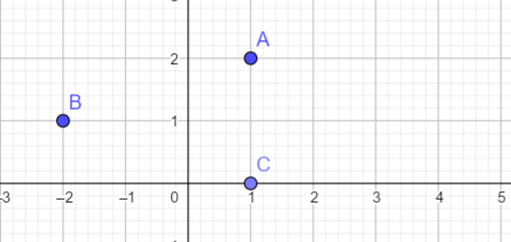
Placer le point $M$ défini par l’égalité vectorielle : $\overrightarrow{AM}=\overrightarrow{BC}$ et lire graphiquement ses coordonnées .

2. a. On note $(x;y)$ les coordonnées du point M, exprimer les coordonnées du vecteur $\overrightarrow{AM}$ en fonction de $x$ et $y$ .

2.b. Calculer les coordonnées du vecteur $\overrightarrow{BC}$ .

2.c. En utilisant le fait que les coordonnées des vecteurs $\overrightarrow{AM}$ et $\overrightarrow{BC}$ sont égales, déterminer les coordonnées de M.