Sommaire
Activité d’approche
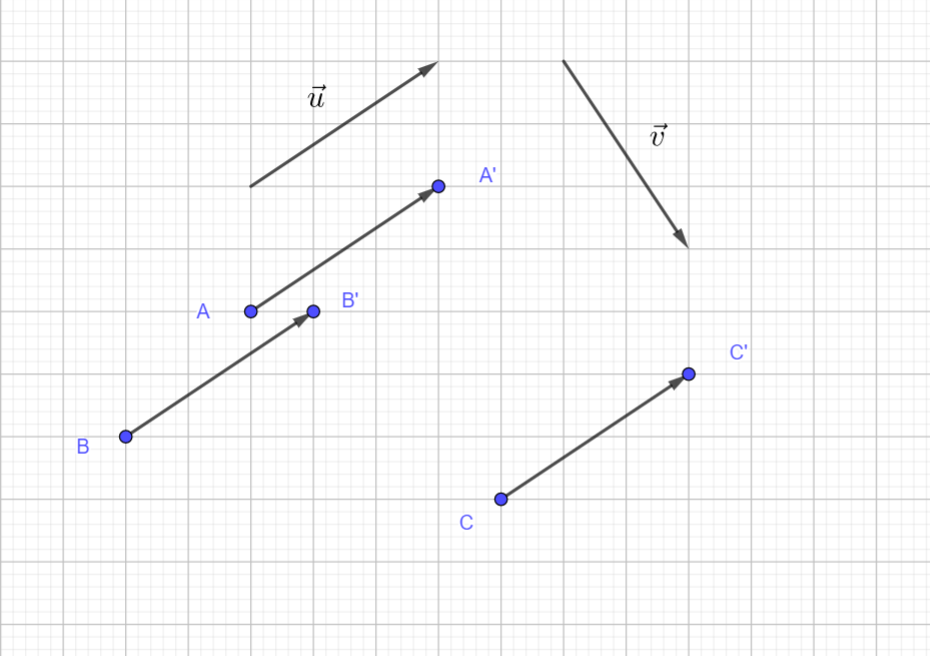
A, B, C sont trois points du plan. \overrightarrow{u} et \overrightarrow{v} sont deux vecteurs.
- Construire A’, B’, C’ les images de A, B, C par la translation de vecteur \vec{u}.
Cliquer sur le troisième onglet en haut, à partir de la gauche et sélectionner Représentant dans le menu déroulant. Dans le repère cliquer sur le point A et sur le vecteur \overrightarrow{u}. Le point A’ s’affiche.
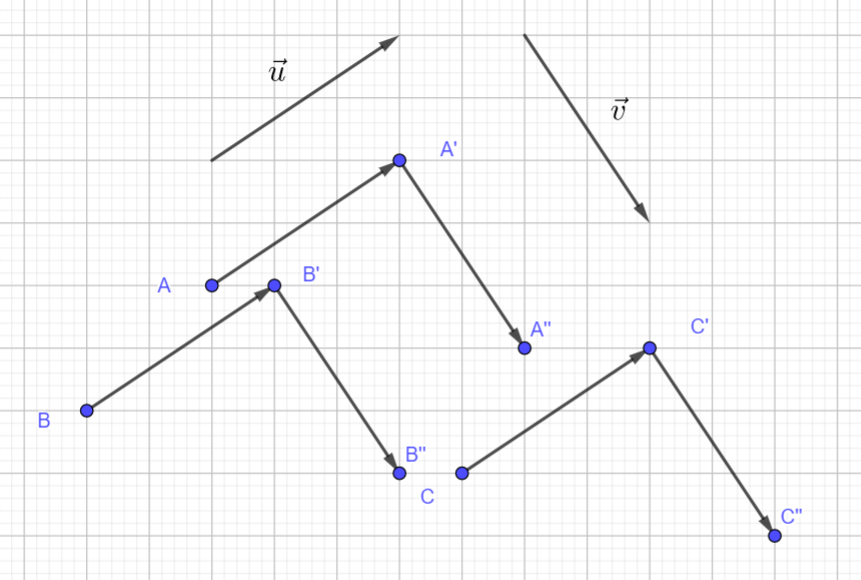
2. Construire A", B", C" les images de A’, B’, C’ par la translation de vecteur \vec{v} .
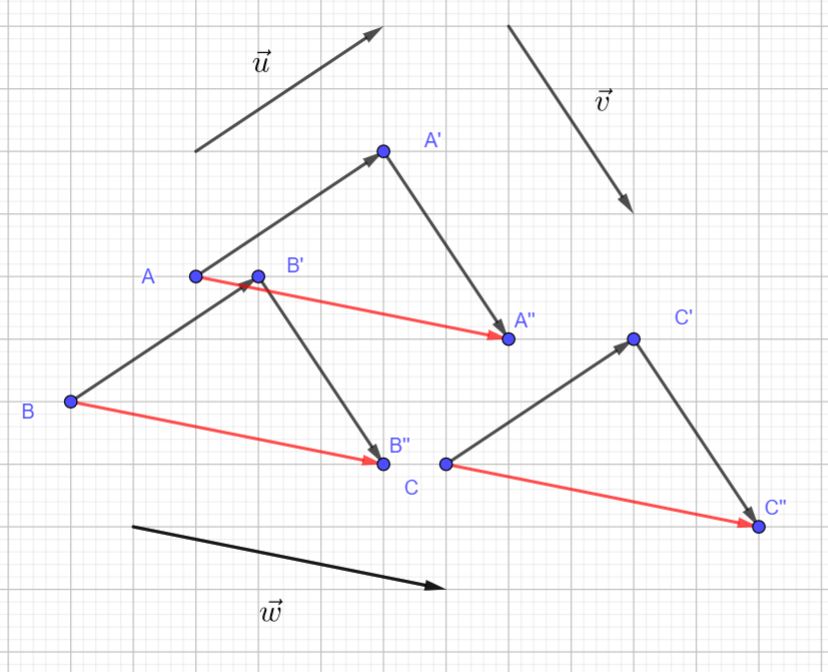
3. Pour obtenir A", B", C" à partir de A, B, C on peut utiliser la translation d’un vecteur \vec{w}. Dessiner ce vecteur \vec{w} sur la figure.
Cliquer sur le troisième onglet en haut, à partir de la gauche et sélectionner Vecteur dans le menu déroulant. Dans le repère cliquer sur le point A et sur le point A". Le vecteur \overrightarrow{AA"} s’affiche.
4. Synthèse :Pour obtenir A", B", C" à partir de A, B, C nous avons tout d’abord utiliser deux translations l’une après l’autre.
Puis nous avons vu que l’on peut utiliser la translation d’un vecteur \vec{w}.
La somme des vecteurs \vec{u} et \vec{v} notée \vec{u}+\vec{v} est égale à \vec{w}. On note \vec{u}+\vec{v}=\vec{w}
Remarque : \overrightarrow{AA’}+ \overrightarrow{A’A"}= \overrightarrow{AA"}\\\hspace{1.4cm} \overrightarrow{BB’}+ \overrightarrow{B’B"}= \overrightarrow{BB"}\\\hspace{1.4cm} \overrightarrow{CC’}+ \overrightarrow{C’C"}= \overrightarrow{CC"}
Somme de deux vecteurs
Définition
Si on enchaîne deux translations de vecteurs \vec{u} et \vec{v} , on obtient une nouvelle translation dont le vecteur est, par définition, la somme des vecteurs \vec{u} et \vec{v} noté \vec{u}+\vec{v}.
Relation de Chasles
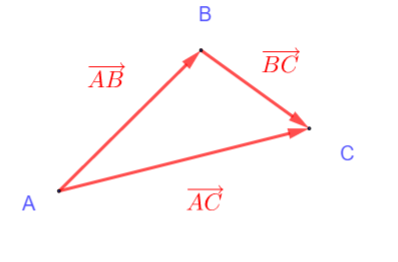
quelque soient les points A, B, C on a la relation suivante \overrightarrow{AB}+ \overrightarrow{BC}= \overrightarrow{AC}
Méthode
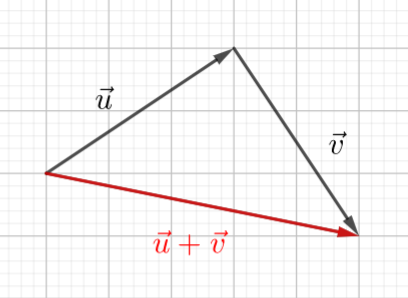
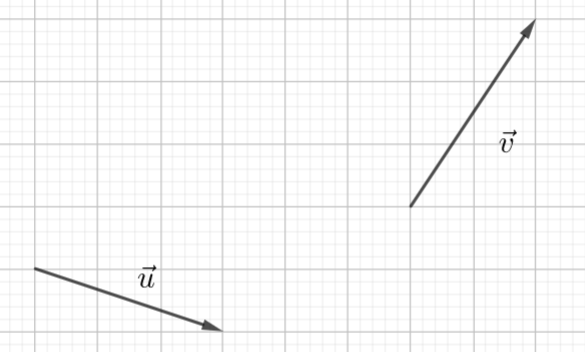
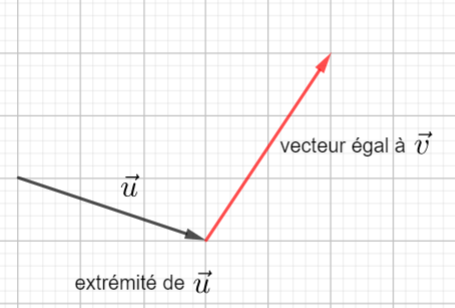
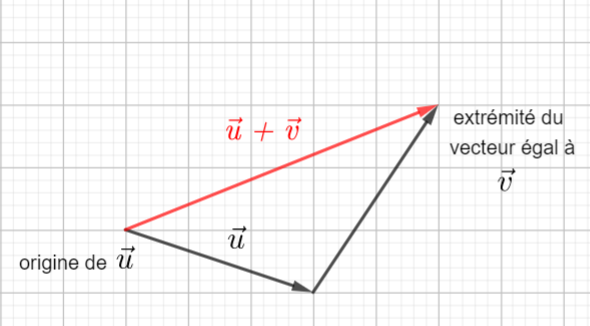
Pour construire la somme de deux vecteurs \vec{u}+\vec{v}, je construis un vecteur égal au vecteur \vec{v} à partir de l’extrémité du vecteur \vec{u} . Puis je trace le vecteur qui a pour origine l’origine du vecteur \vec{u} et pour extrémité l’extrémité du vecteur égal au vecteur \vec{v} que l’on vient de tracer.
Exercice n°1
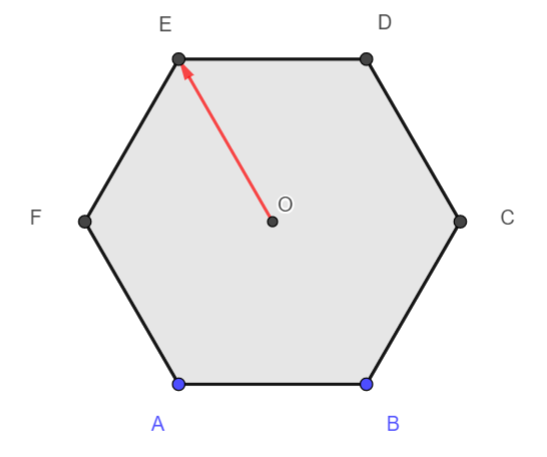
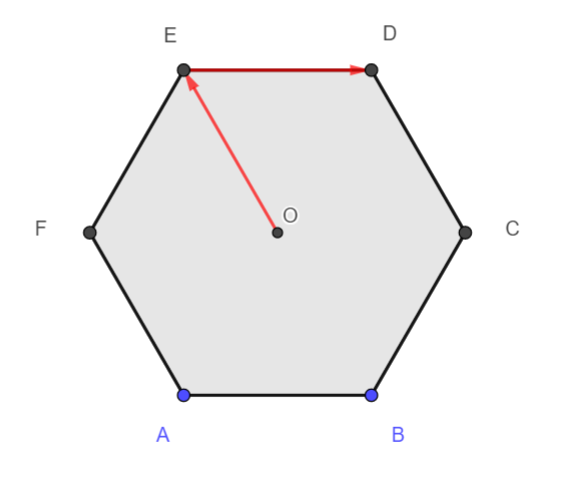
ABCDEF est un hexagone régulier de centre O
Compléter les pointillés dans chaque cas:
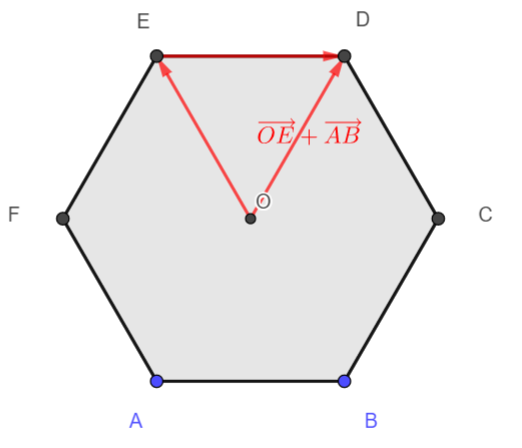
- \overrightarrow{OE}+ \overrightarrow{AB}= \overrightarrow{O…}
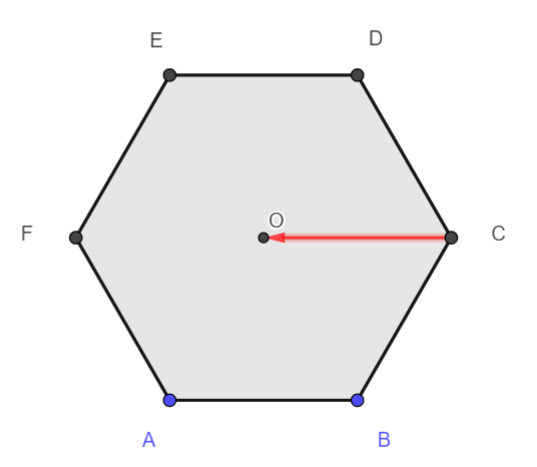
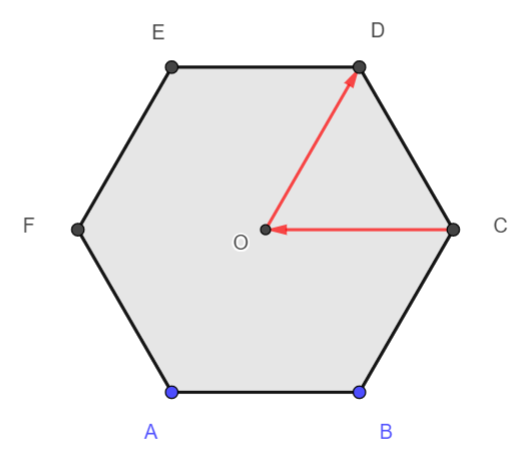
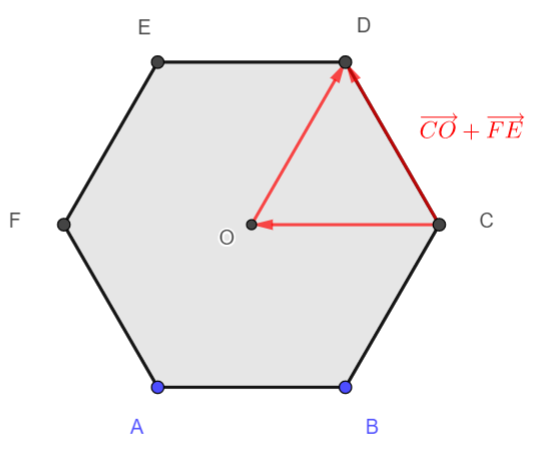
2. \overrightarrow{CO}+ \overrightarrow{FE}= \overrightarrow{C…}
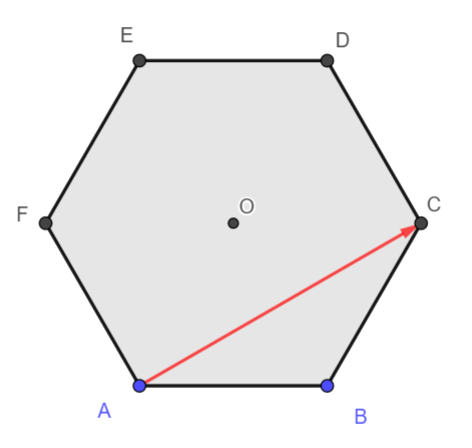
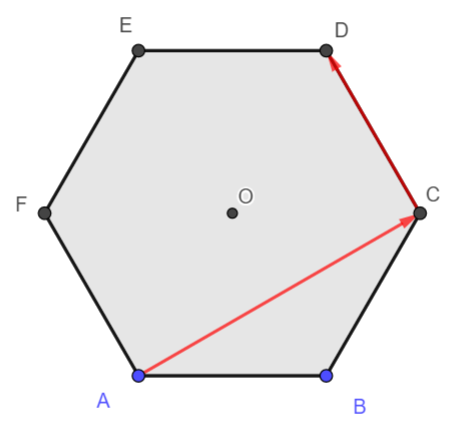
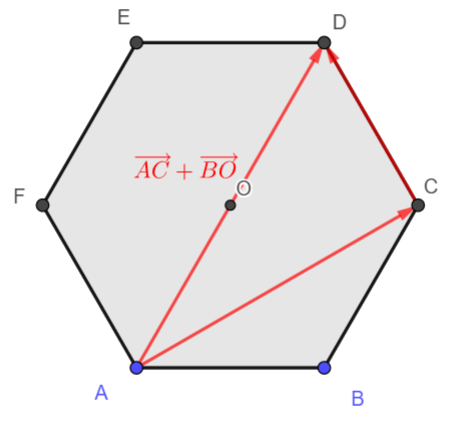
3. \overrightarrow{AC}+ \overrightarrow{BO}= \overrightarrow{A…}
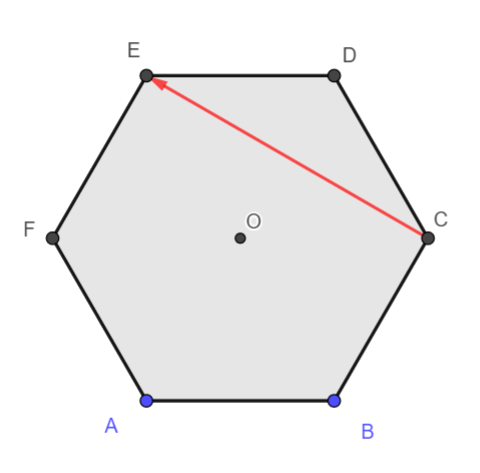
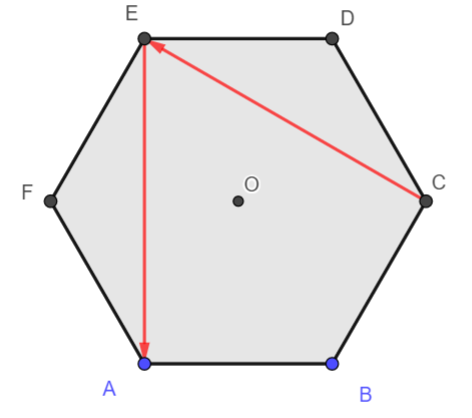
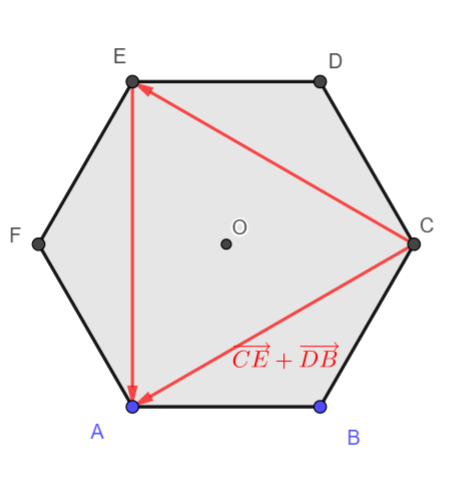
4. \overrightarrow{CE}+ \overrightarrow{DB}= \overrightarrow{C…}
Propriétés
\vec{u}+\vec{v}= \vec{v}+\vec{u}\\ (\vec{u}+\vec{v})+\vec{w}= \vec{u}+(\vec{v}+\vec{w})\\ \vec{u}+\vec{0}= \vec{0}+\vec{u}=\vec{u}\\ \vec{u}+(-\vec{u})= (-\vec{u})+\vec{u}=\vec{0}\\ \overrightarrow{AA}=\overrightarrow{BB}=\overrightarrow{CC}=\vec{0}\\ \overrightarrow{BA}=-\overrightarrow{AB}coordonnées de la somme de deux vecteurs
Propriété
si \vec{u} a pour coordonnées (a;b) et si \vec{v} a pour coordonnées (a’;b’)
alors \vec{u}+\vec{v} a pour coordonnées (a+a’;b+b’)
Exercice n°2
Soient A(4;2) et B(-2;6).
- Calculer les coordonnées de I le milieu de [AB] (utiliser la formule vue dans la partie coordonnées d’un point).
Avant de se lancer dans les calculs, on peut conjecturer les coordonnées du milieu I en utilisant la fenêtre géogébra ci-dessus. Pour cela on clique sur le deuxième onglet en partant de la gauche et on sélectionne Milieu ou centre dans le menu déroulant. Dans le repère on clique gauche sur le point A et sur le point B, le logiciel nomme le milieu C. Pour le renommer on clique droit sur C et on sélectionne Renommer dans le menu déroulant. On renomme le point avec la lettre I. On lit ses coordonnées dans la colonne Algèbre.
2.a.Calculer les coordonnées du vecteur \overrightarrow{IA}.
Avant de se lancer dans les calculs, on peut conjecturer les coordonnées du vecteurs \overrightarrow{IA} en utilisant la fenêtre géogébra ci-dessus. Pour cela on clique sur le troisième onglet en partant de la gauche et on sélectionne Vecteur dans le menu déroulant. Dans le repère on clique gauche sur le point I et sur le point A. On lit ses coordonnées dans la colonne Algèbre.
2.b.Calculer les coordonnées du vecteur \overrightarrow{IB}.
Avant de se lancer dans les calculs, on peut conjecturer les coordonnées du vecteurs \overrightarrow{IB} en utilisant la fenêtre géogébra ci-dessus. Pour cela on clique sur le troisième onglet en partant de la gauche et on sélectionne Vecteur dans le menu déroulant. Dans le repère on clique gauche sur le point I et sur le point B. On lit ses coordonnées dans la colonne Algèbre.
2.c. Calculer les coordonnées du vecteur \overrightarrow{IA} +\overrightarrow{IB}.
2.d. Le résultat de la question 2.c. vous semble-t-il cohérent ?
Exercice n°3
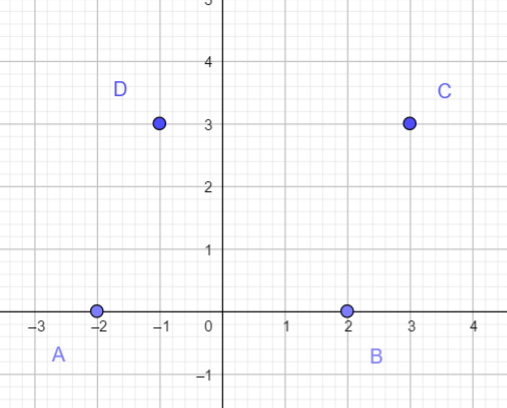
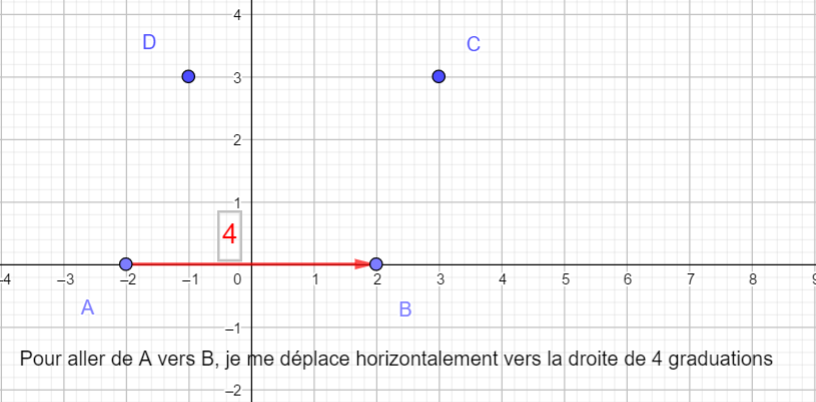
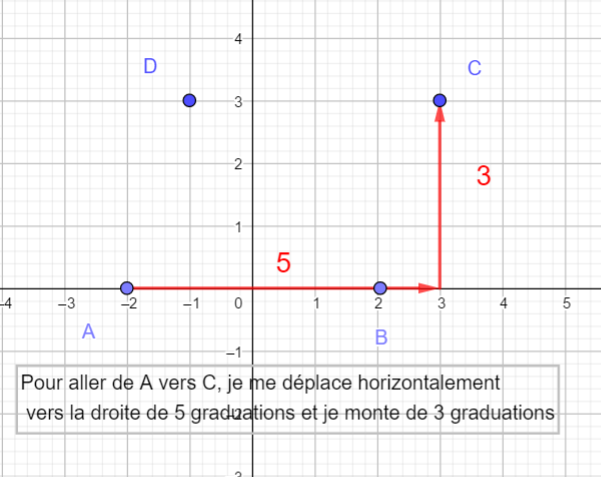
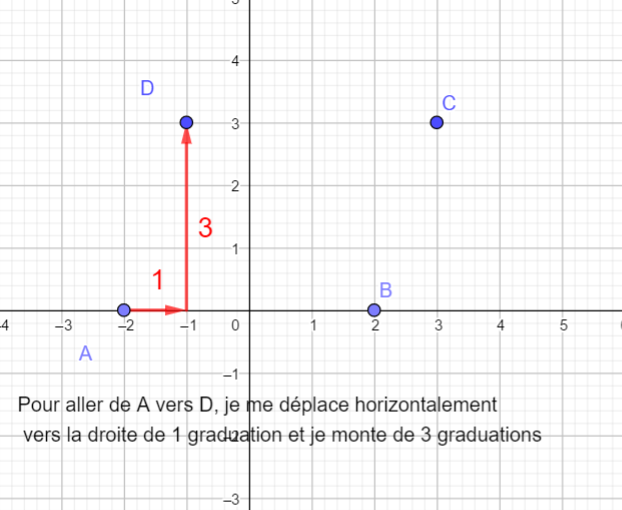
- Lire graphiquement les coordonnées des vecteurs \overrightarrow{AB} , \overrightarrow{AC} et \overrightarrow{AD}
2. Calculer les coordonnées du vecteur \overrightarrow{AB}+\overrightarrow{AD} .
3. Comparez-les avec celle de \overrightarrow{AC}. Qu’en pensez-vous ?