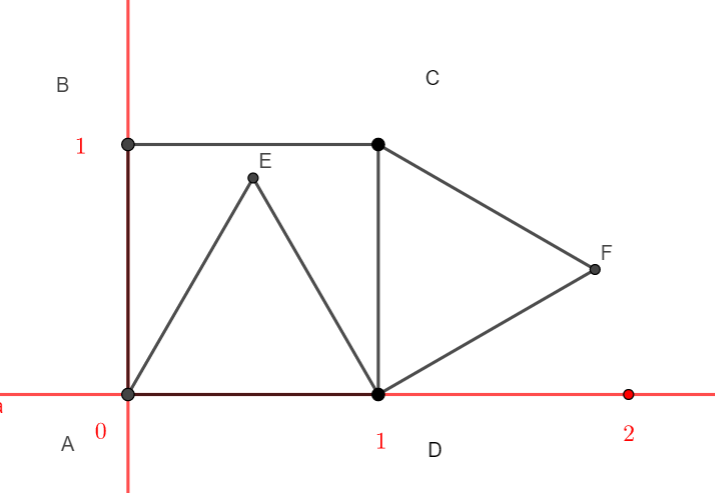
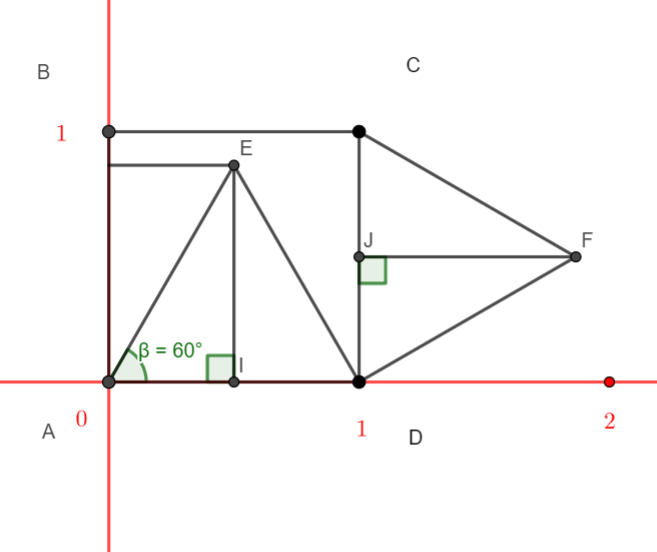
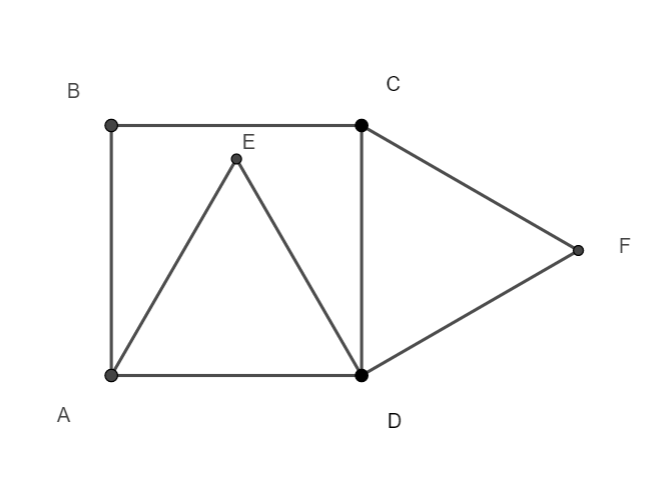
ABCD est un carré de côté 1.
ADE et CDF sont deux triangles équilatéraux.
On veut montrer que les points B, E, F sont alignés.
METHODE 1 : Montrons que les points B, E, F sont alignés en montrant que les vecteurs
\overrightarrow{BE} et \overrightarrow{BF} sont colinéaires en montrant que le déterminant des vecteurs \overrightarrow{BE} et \overrightarrow{BF} est nul.
On choisit le repère orthonormé A;\overrightarrow{AD};\overrightarrow{AB}
1. Lire graphiquement les coordonnées des points \textit{\textbf{A;B;C;D }}.
2. L’objectif de cette question est de déterminer, par le calcul, les coordonnées du point \textit{\textbf{E}} .
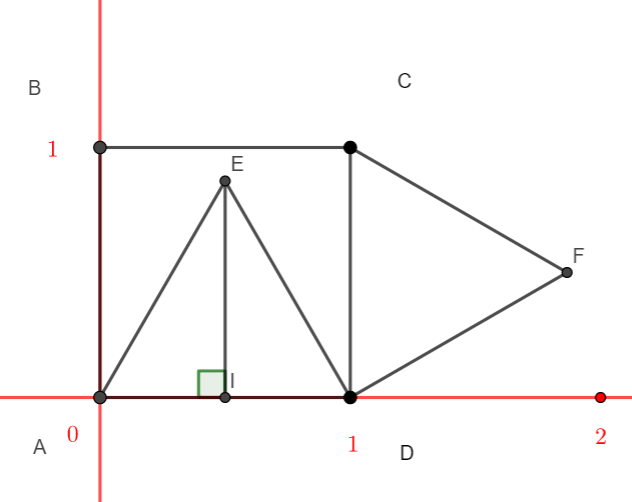
a. On note I le milieu du segment [AD] . Justifier que les droites (EI) et (AD) sont orthogonales. En déduire la nature du triangle AIE .
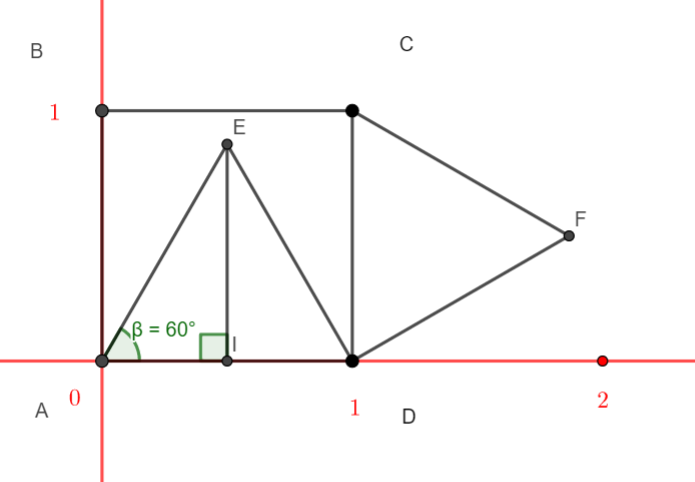
b. Dans le triangle AIE rectangle en I , justifier que l’angle \widehat{IAE} mesure 60°. A l’aide d’une relation trigonométrique dans le triangle AIE rectangle en I , calculer la distance EI .
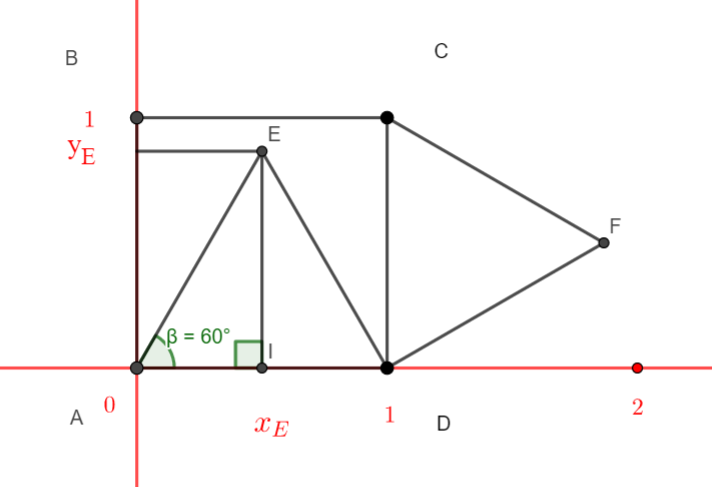
c. Déduire des questions précédentes les coordonnées du point E .
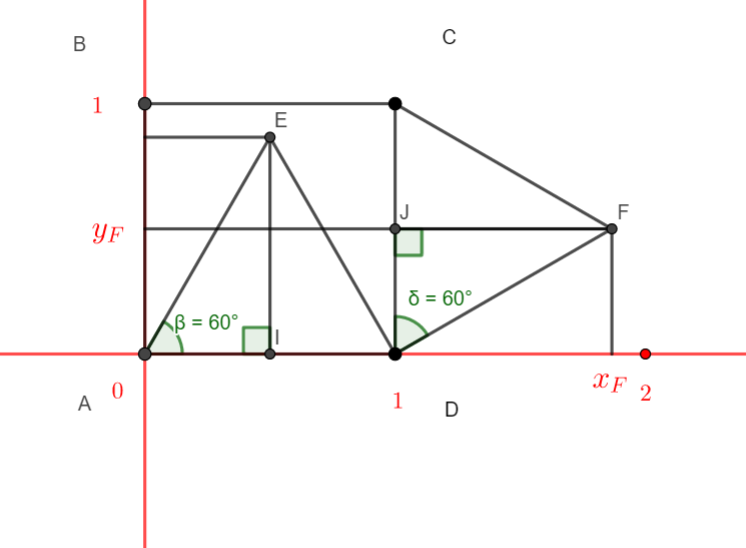
3. L’objectif de cette question est de déterminer, par le calcul, les coordonnées du point \textit{\textbf{F}} .
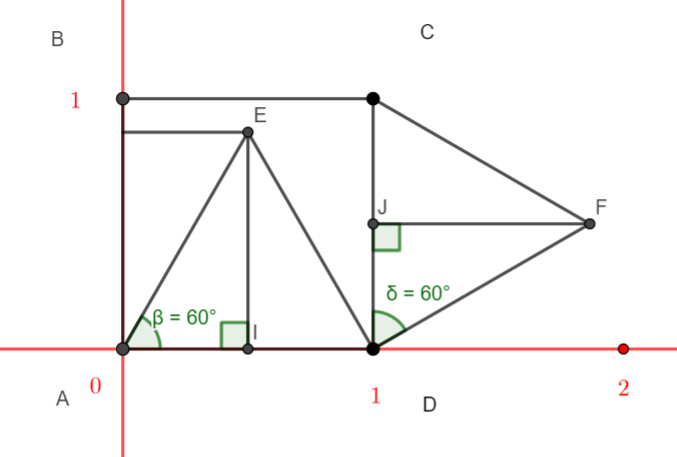
a. On note J le milieu du segment [CD] . Justifier que les droites (FJ) et (CD) sont orthogonales. En déduire la nature du triangle FJD .
b. Dans le triangle FJD rectangle en J , justifier que l’angle \widehat{FDJ} mesure 60°. A l’aide d’une relation trigonométrique dans le triangle FJD rectangle en J , calculer la distance FJ .
c. Déduire des questions précédentes les coordonnées du point F .
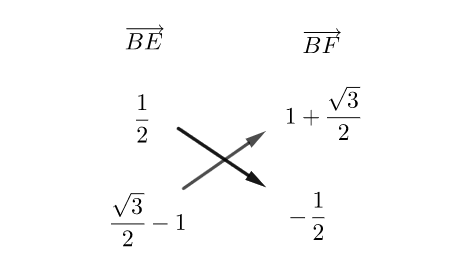
4. a. Déterminer par le calcul les coordonnées du vecteur \overrightarrow{BE} et les coordonnées du vecteur \overrightarrow{BF} .
b. Calculer le déterminant des vecteurs \overrightarrow{BE} et \overrightarrow{BF} .
c. Conclure.
METHODE 2 : Montrons que les points B, E, F sont alignés en montrant que par exemple les coordonnées du point F vérifient l’équation réduite de la droite (BE) .
Remarque : le choix de la droite (BE) n’est pas le fait du hasard, les coordonnées de ces deux points sont moins compliquées que celles de F.
Nous n’allons pas déterminer à nouveau les coordonnées des points de la figure, nous allons nous contenter de les rappeler.
A(0;0),B(0;1),C(1;1),D(1;0),E(\frac{1}{2};\frac{\sqrt{3}}{2}),F(1+ \frac{\sqrt{3}}{2};\frac{1}{2}).
- Déterminer, par le calcul, l’équation réduite de la droite (BE).
2. Montrer que les coordonnées du point F vérifient l’équation réduite de la droite (BE) et conclure.
METHODE 3 : Montrons que les points B, E, F sont alignés en montrant que par exemple les coordonnées du point F vérifient l’équation cartésienne de la droite (BE) .
Remarque : le choix de la droite (BE) n’est pas le fait du hasard, les coordonnées de ces deux points sont moins compliquées que celles de F.
Nous n’allons pas déterminer à nouveau les coordonnées des points de la figure, nous allons nous contenter de les rappeler.
A(0;0),B(0;1),C(1;1),D(1;0),E(\frac{1}{2};\frac{\sqrt{3}}{2}),F(1+ \frac{\sqrt{3}}{2};\frac{1}{2}).
Ainsi que les coordonnées du vecteur \overrightarrow{BE} (\frac{1}{2};1+\frac{\sqrt{3}}{2}).
- Déterminer, par le calcul, une équation cartésienne de la droite (BE).
2. Montrer que les coordonnées du point F vérifient l’équation cartésienne précédente de la droite (BE) et conclure.