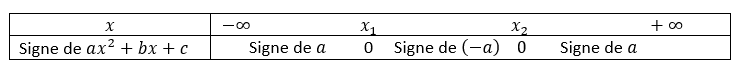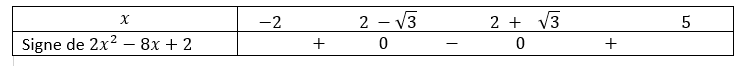Sommaire
Propriété
Soit f une fonction dérivable sur un intervalle I de \mathbf{R}
Si pour tout x de I , f'(x)>0 alors f est strictement croissante sur I.
Si pour tout x de I , f'(x)<0 alors f est strictement décroissante sur I.
Si pour tout x de I , f'(x)=0 alors f est constante sur I.
Exercice n°1
AIDE : Dans cet exercice et les suivants, il faudra calculer f'(x) vous pouvez cliquer sur le bouton ci-dessous pour conjecturer ou vérifier votre résultat.
De plus il faudra étudier le signe de f'(x) vous pouvez cliquer sur le bouton ci-dessous pour conjecturer ou vérifier votre résultat.
Soit la fonction f définie sur [0;4] par f(x)=3x^2-12x+4.
- Calculer f'(x).
2. Etudier le signe de f'(x) sur [0;4].
3. Dresser le tableau de la fonction f sur l’intervalle [0;4].
Exercice n°2
Soit la fonction f définie sur [-4;4] par f(x)=x^3-12x.
- Calculer f'(x).
2. Etudier le signe de f'(x) sur [-4;4].
3. Dresser le tableau de la fonction f sur l’intervalle [-4;4].
Exercice n°3
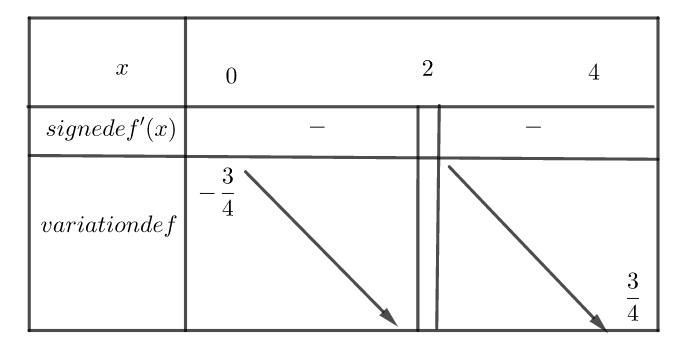
Soit la fonction f définie sur [0;2[\cup]2;4] par f(x)=\frac{3}{2x-4}.
- Calculer f'(x).
2. Etudier le signe de f'(x) sur [0;2[\cup]2;4].
3. Dresser le tableau de la fonction f sur l’intervalle [0;2[\cup]2;4].
Exercice n°4
Soit la fonction f définie sur [-4;4] par f(x)=\sqrt{2x+8}.
- Calculer f'(x).
2. Etudier le signe de f'(x) sur [-4;4].
3. Dresser le tableau de la fonction f sur l’intervalle [-4;4].
Exercice n°5
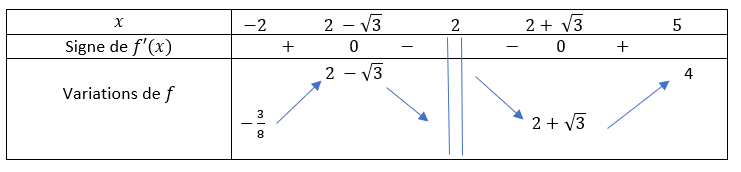
Soit la fonction f définie sur [-2;2[\cup]2;5] par f(x)=\frac{x^2-1}{2x-4}.
- Calculer f'(x).
2. Etudier le signe de f'(x) sur [-2;2[\cup]2;5] .
3. Dresser le tableau de la fonction f sur l’intervalle [-2;2[\cup]2;5] .
Valider les variations avec Géogébra
On saisit par exemple
f(x)=3x^2-12x+4 dans la colonne de gauche et on lit graphiquement les variations de f sur [0;4] puis on compare avec le tableau de variations obtenu.
Si vous ne voyez pas la courbe dans son ensemble, utilisez le 11ème onglet pour déplacer le graphique, agrandir ou réduire.