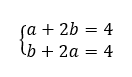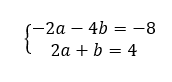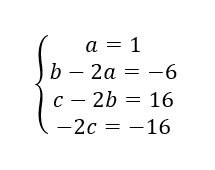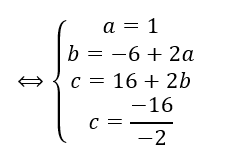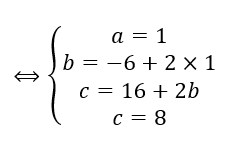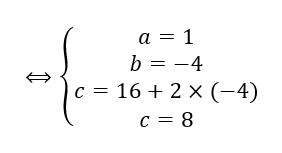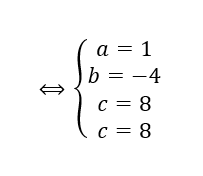logo

TE. Résoudre des équations dans C.

Sommaire

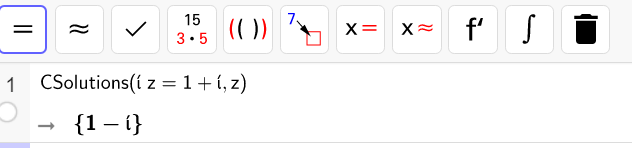
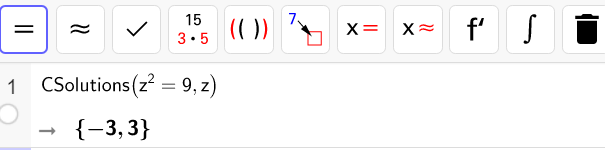
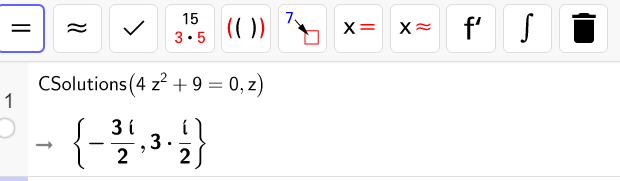
Page de calcul formel de Géogébra pour conjecturer les solutions des équations de cette fiche.

Saisir CSolutions(équation,variable) puis faire entrer. Pout taper i, appuyer sur la touche Alt puis la touche i.

Equations du premier degré ne comportant que la variable z.

Méthode 

On procède comme dans \mathbf{R}, on remet à leur place les membres qui ne sont pas à leur place.

Exemple n°1

Résoudre dans \mathbf{C}, l’équation 2z+1=i.

1.Résolution par le calcul

C’est une équation du premier degré ne comportant que la variable z.

1 n’est pas à sa place dans le membre de gauche. On enlève 1 de chaque côté de l’égalité.

2z=i-1

2 n’est pas à sa place dans le membre de gauche, c’est un facteur dans un produit. On divise par 2 de chaque côté de l’égalité.

z=\frac{i-1}{2}

Il faut maintenant écrire la solution sous forme algébrique.

z=-\frac{1}{2}+\frac{i}{2}

Donc l’ensemble solution est S=\{-\frac{1}{2}+\frac{i}{2}\}

2. On peut vérifier avec Géogébra.

3. On ne peut pas utiliser la TI 83 car les coefficients de cette équation ne sont pas tous réels.

Exercice n°1

Résoudre les équations suivantes dans   \mathbf{C}.

(1-i)z=2+2i
correction
-2iz=2z+3
correction
\frac{z+2}{z-2}=3i
correction
iz=1+i
correction
z=2iz+3
correction
\frac{z-1}{i}=2
correction

Equations du premier degré comportant la variable z et son conjugué.

Méthode 

On pose z=a+ib.

On remplace ensuite z par a+ib et \overline{z} par a-ib dans l’équation.

Enfin on utilise la propriété : deux complexes sont égaux si et seulement si leurs parties réelles sont égales ainsi que leurs parties imaginaires. On obtient alors deux équations du premier degré. Dans la première équation, l’inconnue est a. Dans la deuxième équation, l’inconnue est b.

Il ne reste plus qu’à résoudre l’équation.

Exemple n°2

Résoudre dans \mathbf{C}, l’équation z+2\overline{z}=i.

Résolution par le calcul

C’est une équation du premier degré qui comporte la variable z et le conjugué \overline{z}.

On remplace z par a+ib et \overline{z} par a-ib .

a+ib+2(a-ib)=i

On développe 2(a-ib)

a+ib+2a-2ib=i

On met les deux membres sous forme algébrique

a+2a+ib-2ib=0+1\times i\\3a-ib=0+1\times i

Deux complexes sont égaux si et seulement si leurs parties réelles sont égales ainsi que leurs parties imaginaires.

3a=0  et  -b=1

On résout les équations 

a=0  et  b=-1.

Donc z=0-i\\\hspace{0.8cm}z=-i

Ainsi l’ensemble solution est S=\{-i\}

Exercice n°2

Résoudre les équations suivantes dans   \mathbf{C}.

2z+4\overline{z}+i=3
correction
z+2i \overline{z}=4+4i
correction
\overline{z}=6z-2i
correction

Equations du second degré à coefficients réels.

Théorème :

Soit les réels a,b,c avec a\ne o, pour résoudre l’équation  az²+bz+c=0,

on calcule \Delta=b²-4ac  

si \Delta<0 , l’équation admet deux solutions complexes conjuguées z_1=\frac{-b-i\sqrt{-\Delta}}{2a} et z_2=\overline{z_1}=\frac{-b+i\sqrt{-\Delta}}{2a}

si \Delta=0 , l’équation admet une solution réelle notée z_0=-\frac{b}{2a}

si \Delta>0 , l’équation admet deux solutions réelles notées z_1=\frac{-b-\sqrt{\Delta}}{2a} et z_2=\frac{-b+\sqrt{\Delta}}{2a}

Exemple n°3

On veut résoudre l’équation  z^2-4z+5=0.

 1. Résolution de l’équation  par le calcul.

J’identifie les coefficients l’équation a=1, b=-4 et c=5.

Je calcule \Delta=b²-4ac  en remplaçant a,b,c  par 1, (-4) ,5.

\Delta=(-4)²-4\times{1}\times{5}\\\Delta=16-20\\\Delta=-4

comme \Delta<0 , l’équation admet deux solutions complexes conjuguées z_1=\frac{-b-i\sqrt{-\Delta}}{2a} et z_2=\overline{z_1}=\frac{-b+i\sqrt{-\Delta}}{2a}

Je calcule z_1=\frac{-b-i\sqrt{-\Delta}}{2a} en remplaçant a,b,\Delta  par 1,(-4),(-4).

z_1=\frac{-(-4)-i\sqrt{-(-4)}}{2\times 1}\\z_1=\frac{4-i\sqrt{4}}{2}\\z_1=\frac{4-2i}{2}\\z_1=2-i

Pour calculer z_2, on utilise z_2=\overline{z_1}.

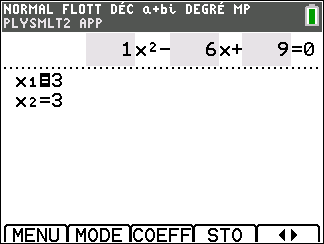
z_2=\overline{z_1}=2+i

Je conclus S=\{2-i;2+i\}

 2. Vérification à l’aide de Géogébra 

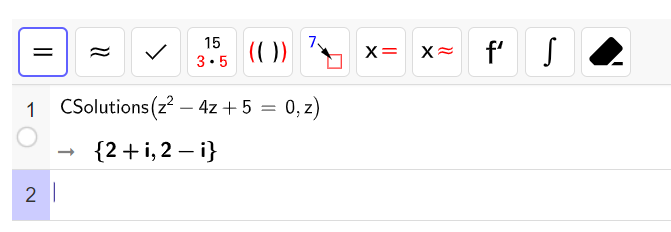
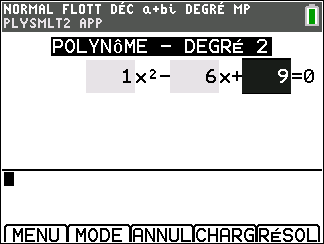
 3. Vérification à l’aide de la TI 83 Premium CE ( on peut utiliser la calculatrice car les coefficients sont réels.

Au clavier

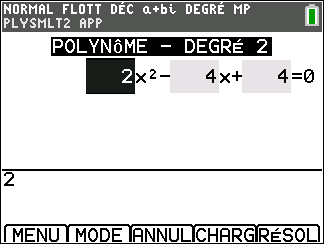
A l’écran

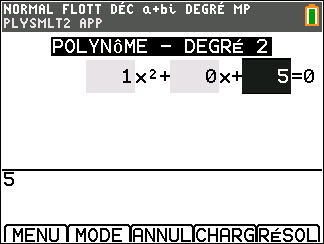
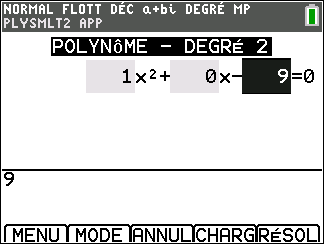
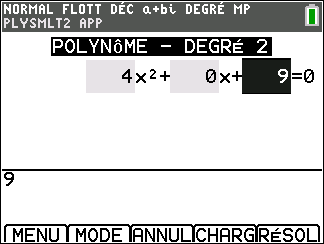
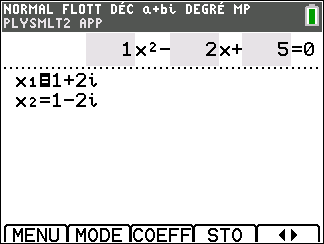
Appuyer sur la touche resol du clavier, sélectionner 2: PlySmlt2 dans le menu déroulant, valider par entrer puis sélectionner 1: RACINES D’UN POLYNOME valider par entrer. Sélectionner le degré du polynôme, ici 2. Sélectionner a+bi. 

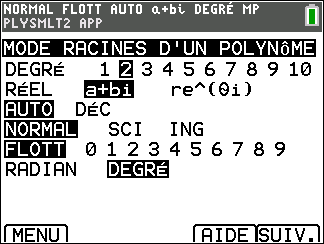
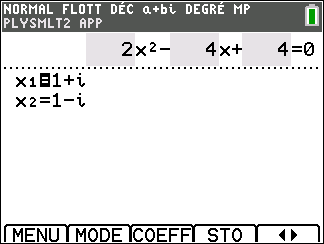
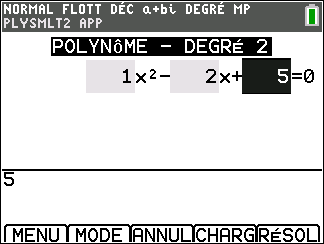
Appuyer sur la touche graph du clavier ( située sous SUIV de l’écran ), saisir l’équation. Attention, après avoir saisi le coefficient ou l’opération, toujours valider par entrer.   

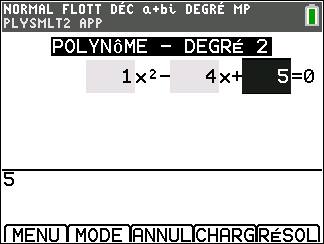
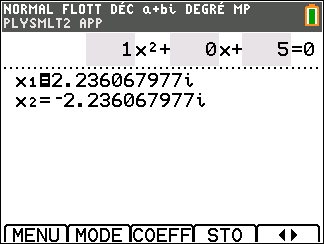
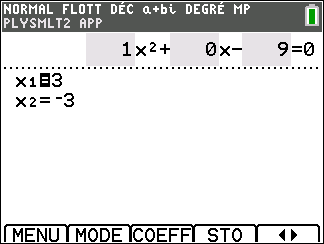
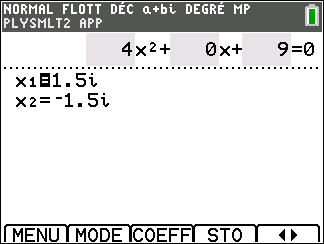
Appuyer sur la touche graph ( située sous RESOL de l’écran ) clavier, les solutions apparaissent.

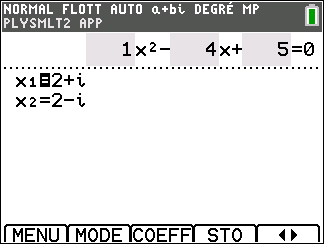
Exercice n°3

Résoudre les équations suivantes dans   \mathbf{C}.

2z^2-4z+4=0
correction
z^2+5=0
correction
z^2=9
correction
z^2=6z-9
correction
4z^2+9=0
correction
z^2+5=2z
correction

Quelques équations de degré supérieur à 2 à coefficients réels.

Méthode ( pour résoudre une équation de degré 3 dont on connaît une racine : a)

étape n°1 : on fait tout passer à gauche, zéro apparaît à droite.

étape n°2 : on  factorise le membre de gauche par z-a.

étape n°3 : on  applique la règle du produit nul.

Exemple n°4

On veut résoudre l’équation  z^3-2z^2+z-2=0.

1.Vérifier que 2 est une solution de l’équation.

On remplace tous les z par 2 et on s’assure que l’égalité est vérifiée.

2^3-2\times 2^2+2-2=8-2\times 4+2-2\\\hspace{3cm}=8-8+2-2\\\hspace{3cm}=0

Donc 2 est une solution de l’équation.

2. Déterminer a,b,c tels que z^3-2z^2+z-2=(z-2)(az^2+bz+c)

On écrit l’égalité dans l’autre sens.

(z-2)(az^2+bz+c)=z^3-2z^2+z-2

On développe le membre de gauche.

az^3+bz^2+cz-2az^2-2bz-2c=z^3-2z^2+z-2

On ordonne le membre de gauche suivant les puissances décroissantes.

az^3+(b-2a)z^2+z(c-2b)-2c=z^3-2z^2+z-2

On identifie les coefficients.

Les coefficients de z^3 sont égaux :a=1

Les coefficients de z^2 sont égaux :b-2a=-2

Les coefficients de z sont égaux :c-2b=1

Les coefficients constants sont égaux :-2c=-2 

On résout le système :

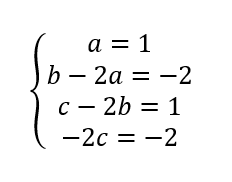
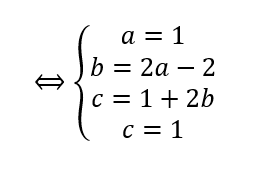
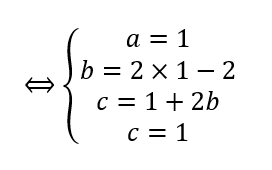
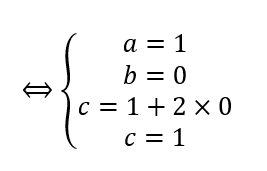
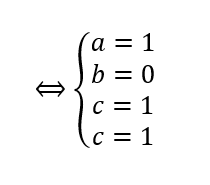
Donc z^3-2z^2+z-2=(z-2)(1\times z^2+0\times z+1)

Ou z^3-2z^2+z-2=(z-2)( z^2+1)

3. Déterminer toutes les solutions de l’équation.

(z-2)( z^2+1)=0

On applique la règle du produit nul

Le premier facteur est nul

z-2=0

C’est une équation du premier degré, on remet les membres à leur place.

z=2

Le second facteur est nul

z^2+1=0

J’identifie les coefficients l’équation a=1, b=0 et c=1.

Je calcule \Delta=b²-4ac  en remplaçant a,b,c  par 1,0 ,1.

\Delta=0²-4\times{1}\times{1}\\\Delta=0-4\\\Delta=-4

comme \Delta<0 , l’équation admet deux solutions complexes conjuguées z_1=\frac{-b-i\sqrt{-\Delta}}{2a} et z_2=\overline{z_1}=\frac{-b+i\sqrt{-\Delta}}{2a}

Je calcule z_1=\frac{-b-i\sqrt{-\Delta}}{2a} en remplaçant a,b,\Delta  par 1,0,(-4).

z_1=\frac{-0-i\sqrt{-(-4)}}{2\times 1}\\z_1=\frac{0-i\sqrt{4}}{2}\\z_1=\frac{-2i}{2}\\z_1=-i

Pour calculer z_2, on utilise z_2=\overline{z_1}.

z_2=\overline{z_1}=i

Je conclus S=\{2;-i;i\}

Exercice n°4

On veut résoudre l’équation  z^3-6z^2+16z-16=0.

1.Vérifier que 2 est une solution de l’équation.

correction

2. Déterminer a,b,c tels que z^3-6z^2+16z-16=(z-2)(az^2+bz+c)

correction

3. Déterminer toutes les solutions de l’équation.

correction

©2020 – Math’O karé SAS

Résoudre dans \mathbf{C}, l’équation (1-i)z=2+2i.

1.Résolution par le calcul

C’est une équation du premier degré ne comportant que la variable z.

1-i n’est pas à sa place dans le membre de gauche. C’est un facteur dans un produit, on divise par 1-i de chaque côté de l’égalité.

z=\frac{2+2i}{1-i}

On va multiplier par le conjugué du dénominateur 1-i c’est-à-dire 1+i en haut et en bas.

z=\frac{2+2i}{1-i}\times \frac{1+i}{1+i} \\z=\frac{(2+2i)(1+i)}{(1-i)(1+i)}

On utilise l’identité remarquable (a-b)(a+b)=a^2-b^2 pour développer le dénominateur.

z=\frac{2+2i+2i+2i^2}{1^2-i^2}\\z=\frac{2+2i+2i+2\times(-1)}{1-(-1)}\\z=\frac{2+2i+2i-2}{1-(-1)}\\z=\frac{4i}{2}\\z=2i

Donc l’ensemble solution est S=\{2i\}

2. On peut vérifier avec Géogébra.

3. On ne peut pas utiliser la TI 83 car les coefficients de cette équation ne sont pas tous réels.

Résoudre dans \mathbf{C}, l’équation -2iz=2z+3.

1.Résolution par le calcul

C’est une équation du premier degré ne comportant que la variable z.

2z n’est pas à sa place dans le membre de droite. On enlève 2z de chaque côté de l’égalité.

-2iz-2z=3

On met z en facteur dans le membre de gauche.

z(-2i-2)=3

-2-2i n’est pas à sa place dans le membre de gauche. C’est un facteur dans un produit, on divise par -2-2i de chaque côté de l’égalité.

z=\frac{3}{-2-2i}

On va multiplier par le conjugué du dénominateur -2-2i c’est-à-dire -2+2i en haut et en bas.

z=\frac{3}{-2-2i}\times \frac{-2+2i}{-2+2i} \\z=\frac{3(-2+2i)}{(-2-2i)(-2+2i)}

On utilise l’identité remarquable (a-b)(a+b)=a^2-b^2 pour développer le dénominateur.

z=\frac{-6+6i}{(-2)^2-(2i)^2}\\z=\frac{-6+6i}{4-4i^2}\\z=\frac{-6+6i}{4-4\times(-1)}\\z=\frac{-6+6i}{4+4}\\z=\frac{-6+6i}{8}\\z=-\frac{6}{8}+\frac{6}{8}i\\z=-\frac{3}{4}+\frac{3}{4}i

Donc l’ensemble solution est S=\{-\frac{3}{4}+\frac{3}{4}i\}

2. On peut vérifier avec Géogébra.

3. On ne peut pas utiliser la TI 83 car les coefficients de cette équation ne sont pas tous réels.

Résoudre dans \mathbf{C}, l’équation \frac{z+2}{z-2}=3i.

1.Résolution par le calcul

C’est une équation du premier degré ne comportant que la variable z.

On fait le produit en croix.

z+2=3i\times (z-2)\\z+2=3iz-6i

3iz n’est pas à sa place dans le membre de droite. On enlève 3iz de chaque côté de l’égalité.

z+2-3iz=-6i

2 n’est pas à sa place dans le membre de gauche. On enlève 2 de chaque côté de l’égalité.

z-3iz=-6i-2

On met z en facteur dans le membre de gauche.

z(1-3i)=-2-6i

1-3i n’est pas à sa place dans le membre de gauche. C’est un facteur dans un produit, on divise par 1-3i de chaque côté de l’égalité.

z=\frac{-2-6i}{1-3i}

On va multiplier par le conjugué du dénominateur 1-3i c’est-à-dire 1+3i en haut et en bas.

z=\frac{-2-6i}{1-3i}\times \frac{1+3i}{1+3i} \\z=\frac{(-2-6i)(1+3i)}{(1-3i)(1+3i)}

On utilise l’identité remarquable (a-b)(a+b)=a^2-b^2 pour développer le dénominateur.

z=\frac{-2-6i-6i-18i^2}{1^2-(3i)^2}\\z=\frac{-2-12i-18\times(-1)}{1-9i^2}\\z=\frac{-2-12i+18}{1-9\times(-1)}\\z=\frac{16-12i}{1+9}\\z=\frac{16-12i}{10}\\z=\frac{16}{10}-\frac{12}{10}i\\z=\frac{8}{5}-\frac{6}{5}i

Donc l’ensemble solution est S=\{\frac{8}{5}-\frac{6}{5}i\}

2. On peut vérifier avec Géogébra.

3. On ne peut pas utiliser la TI 83 car les coefficients de cette équation ne sont pas tous réels.

Résoudre dans \mathbf{C}, l’équation iz=1+i.

1.Résolution par le calcul

C’est une équation du premier degré ne comportant que la variable z.

i n’est pas à sa place dans le membre de gauche. C’est un facteur dans un produit, on divise par i de chaque côté de l’égalité.

z=\frac{1+i}{i}

On va multiplier par le conjugué du dénominateur i c’est-à-dire -i en haut et en bas.

z=\frac{1+i}{i}\times \frac{-i}{-i} \\z=\frac{(1+i)(-i)}{(i)(-i)}\\z=\frac{-i-i^2}{-i^2}\\z=\frac{-i-(-1)}{-(-1)}\\z=\frac{-i+1}{1}\\z=1-i

2. On peut vérifier avec Géogébra.

3. On ne peut pas utiliser la TI 83 car les coefficients de cette équation ne sont pas tous réels.

Résoudre dans \mathbf{C}, l’équation z=2iz+3.

1.Résolution par le calcul

C’est une équation du premier degré ne comportant que la variable z.

2iz n’est pas à sa place dans le membre de droite. On enlève 2iz de chaque côté de l’égalité.

z-2iz=3

On met z en facteur dans le membre de gauche.

z(1-2i)=3

1-2i n’est pas à sa place dans le membre de gauche. C’est un facteur dans un produit, on divise par 1-2i de chaque côté de l’égalité.

z=\frac{3}{1-2i}

On va multiplier par le conjugué du dénominateur 1-2i c’est-à-dire 1+2i en haut et en bas.

z=\frac{3}{1-2i}\times \frac{1+2i}{1+2i} \\z=\frac{3(1+2i)}{(1-2i)(1+2i)}

On utilise l’identité remarquable (a-b)(a+b)=a^2-b^2 pour développer le dénominateur.

z=\frac{3+6i}{1^2-(2i)^2}\\z=\frac{3+6i}{1-4i^2}\\z=\frac{3+6i}{1-4\times(-1)}\\z=\frac{3+6i}{1+4}\\z=\frac{3+6i}{5}\\z=\frac{3}{5}+\frac{6}{5}i

Donc l’ensemble solution est S=\{\frac{3}{5}+\frac{6}{5}i\}

2. On peut vérifier avec Géogébra.

3. On ne peut pas utiliser la TI 83 car les coefficients de cette équation ne sont pas tous réels.

Résoudre dans \mathbf{C}, l’équation \frac{z-1}{i}=2.

1.Résolution par le calcul

C’est une équation du premier degré ne comportant que la variable z.

i n’est pas à sa place dans le membre de gauche. Le contraire de diviser par i est multiplier par i.  

z-1=2i

-1 n’est pas à sa place dans le membre de gauche. Il faut ajouter 1 de chaque côté.

z=1+2i

Donc l’ensemble solution est S=\{1+2i\}

2. On peut vérifier avec Géogébra.

3. On ne peut pas utiliser la TI 83 car les coefficients de cette équation ne sont pas tous réels.

Résoudre dans \mathbf{C}, l’équation 2z+4\overline{z}+i=3.

Résolution par le calcul

C’est une équation du premier degré qui comporte la variable z et le conjugué \overline{z}.

On remplace z par a+ib et \overline{z} par a-ib .

2(a+ib)+4(a-ib)+i=3

On développe 2(a+ib) et 4(a-ib)

2a+2ib+4a-4ib+i=3

On réduit.

6a-2ib+i=3

On met les deux membres sous forme algébrique

6a+i(-2b+1)=3+0\times i

Deux complexes sont égaux si et seulement si leurs parties réelles sont égales ainsi que leurs parties imaginaires.

6a=3  et  -2b+1=0

On résout les équations 

a=\frac{3}{6}  et  -2b=-1.

a=\frac{1}{2}  et  b=\frac{-1}{-2}.

a=\frac{1}{2}  et  b=\frac{1}{2}.

Donc z=\frac{1}{2}+\frac{1}{2}i

Ainsi l’ensemble solution est S=\{\frac{1}{2}+\frac{1}{2}i\}

 

 

Résoudre dans \mathbf{C}, l’équation z+2i\overline{z}=4+4i.

Résolution par le calcul

C’est une équation du premier degré qui comporte la variable z et le conjugué \overline{z}.

On remplace z par a+ib et \overline{z} par a-ib .

a+ib+2i(a-ib)=4+4i

On développe  2i(a-ib)

a+ib+2ia-2i^2b=4+4i\\a+ib+2ia-2\times(-1)\times b=4+4i\\a+ib+2ia+2b=4+4i

On met les deux membres sous forme algébrique

a+2b+i(b+2a)=4+4i

Deux complexes sont égaux si et seulement si leurs parties réelles sont égales ainsi que leurs parties imaginaires.

a+2b=4  et  b+2a=4

On résout le système d’équations suivant 

On veut éliminer l’inconnue  a, pour cela : on multiplie la première équation par -2 puis on ajoute les deux nouvelles équations.

En ajoutant, on obtient :

-2a-4b+2a+b=-8+4\\-3b=-4\\b=\frac{-4}{-3}\\b=\frac{4}{3}

Pour trouver a on peut remplacer b par \frac{4}{3} dans la première équation du système de départ.

a+2\times \frac{4}{3}=4\\a+ \frac{8}{3}=4\\a=4-\frac{8}{3}\\a=4\times \frac{3}{3}-\frac{8}{3}\\a= \frac{12}{3}-\frac{8}{3}\\a= \frac{4}{3}

Donc z=\frac{4}{3}+\frac{4}{3}i

Ainsi l’ensemble solution est S=\{\frac{4}{3}+\frac{4}{3}i\}

 

 

Résoudre dans \mathbf{C}, l’équation \overline{z}=6z-2i.

Résolution par le calcul

C’est une équation du premier degré qui comporte la variable z et le conjugué \overline{z}.

On remplace z par a+ib et \overline{z} par a-ib .

a-ib=6(a+ib)-2i

On développe 6(a+ib).

a-ib=6a+6ib-2i

On met les deux membres sous forme algébrique

a-ib=6a+i(6b-2)

Deux complexes sont égaux si et seulement si leurs parties réelles sont égales ainsi que leurs parties imaginaires.

a=6a  et  -b=6b-2

On résout les équations 

a-5a=0  et  -b-6b=-2.

-4a=0  et  -7b=-2.

a=\frac{0}{-4}  et  b=\frac{-2}{-7}.

a=0  et  b=\frac{2}{7}.

Donc z=\frac{2}{7}i

Ainsi l’ensemble solution est S=\{\frac{2}{7}i\}

 

 

On veut résoudre l’équation  2z^2-4z+4=0.

 1. Résolution de l’équation  par le calcul.

J’identifie les coefficients l’équation a=2, b=-4 et c=4.

Je calcule \Delta=b²-4ac  en remplaçant a,b,c  par 2, (-4) ,4.

\Delta=(-4)²-4\times{2}\times{4}\\\Delta=16-32\\\Delta=-16

comme \Delta<0 , l’équation admet deux solutions complexes conjuguées z_1=\frac{-b-i\sqrt{-\Delta}}{2a} et z_2=\overline{z_1}=\frac{-b+i\sqrt{-\Delta}}{2a}

Je calcule z_1=\frac{-b-i\sqrt{-\Delta}}{2a} en remplaçant a,b,\Delta  par 2,(-4),(-16).

z_1=\frac{-(-4)-i\sqrt{-(-16)}}{2\times 2}\\z_1=\frac{4-i\sqrt{16}}{4}\\z_1=\frac{4-4i}{4}\\z_1=1-i

Pour calculer z_2, on utilise z_2=\overline{z_1}.

z_2=\overline{z_1}=1+i

Je conclus S=\{1-i;1+i\}

 2. Vérification à l’aide de Géogébra 

3. Vérification à l’aide de la TI 83 Premium CE ( on peut utiliser la calculatrice car tous les coefficients sont réels ).

Au clavier

A l’écran

Appuyer sur la touche resol du clavier, sélectionner 2: PlySmlt2 dans le menu déroulant, valider par entrer puis sélectionner 1: RACINES D’UN POLYNOME valider par entrer. Sélectionner le degré du polynôme, ici 2. Sélectionner a+bi. 

Appuyer sur la touche graph du clavier ( située sous SUIV de l’écran ), saisir l’équation. Attention, après avoir saisi le coefficient ou l’opération, toujours valider par entrer.   

Appuyer sur la touche graph ( située sous RESOL de l’écran ) clavier, les solutions apparaissent.

On veut résoudre l’équation  z^2+5=0.

 1. Résolution de l’équation  par le calcul méthode n°1 (celle vue dans l’exemple).

C’est une équation du second degré d’inconnue z.

J’identifie les coefficients l’équation a=1, b=0 et c=5.

Je calcule \Delta=b²-4ac  en remplaçant a,b,c  par 1, 0 ,5.

\Delta=0²-4\times{1}\times{5}\\\Delta=0-20\\\Delta=-20

comme \Delta<0 , l’équation admet deux solutions complexes conjuguées z_1=\frac{-b-i\sqrt{-\Delta}}{2a} et z_2=\overline{z_1}=\frac{-b+i\sqrt{-\Delta}}{2a}

Je calcule z_1=\frac{-b-i\sqrt{-\Delta}}{2a} en remplaçant a,b,\Delta  par 1,0,(-20).

z_1=\frac{-0-i\sqrt{-(-20)}}{2\times 1}\\z_1=\frac{-i\sqrt{20}}{2}\\z_1=-\frac{2\sqrt{5}}{2}i\\z_1=-\sqrt{5}i

Pour calculer z_2, on utilise z_2=\overline{z_1}.

z_2=\overline{z_1}=\sqrt{5}i

Je conclus S=\{-\sqrt{5}i;\sqrt{5}i\}

Résolution de l’équation  par le calcul méthode n°2 ( plus rapide).

z^2+5=0\\z^2=-5\\z^2=(-1)\times 5\\z^2=i^2\times {\sqrt{5}^2}\\z^2=(i\sqrt{5})^2\\z=-i\sqrt{5} ou z=i\sqrt{5}

Je conclus S=\{-\sqrt{5}i;\sqrt{5}i\}

 2. Vérification à l’aide de Géogébra 

3. Vérification à l’aide de la TI 83 Premium CE ( on peut utiliser la calculatrice car tous les coefficients sont réels ).

Au clavier

A l’écran

Appuyer sur la touche resol du clavier, sélectionner 2: PlySmlt2 dans le menu déroulant, valider par entrer puis sélectionner 1: RACINES D’UN POLYNOME valider par entrer. Sélectionner le degré du polynôme, ici 2. Sélectionner a+bi. 

Appuyer sur la touche graph du clavier ( située sous SUIV de l’écran ), saisir l’équation. Attention, après avoir saisi le coefficient ou l’opération, toujours valider par entrer.   

Appuyer sur la touche graph ( située sous RESOL de l’écran ) clavier, les solutions apparaissent.

On veut résoudre l’équation  z^2=9 ou z^2-9=0 .

 1. Résolution de l’équation  par le calcul méthode n°1 (celle vue dans l’exemple).

C’est une équation du second degré d’inconnue z.

J’identifie les coefficients l’équation a=1, b=0 et c=-9.

Je calcule \Delta=b²-4ac  en remplaçant a,b,c  par 1, 0 ,(-9).

\Delta=0²-4\times{1}\times{(-9)}\\\Delta=0-(-36)\\\Delta=36

comme \Delta>0 , l’équation admet deux solutions réelles z_1=\frac{-b-\sqrt{\Delta}}{2a} et z_2=\frac{-b+\sqrt{\Delta}}{2a}

Je calcule z_1=\frac{-b-\sqrt{\Delta}}{2a} en remplaçant a,b,\Delta  par 1,0,36.

z_1=\frac{-0-\sqrt{36}}{2\times 1}\\z_1=\frac{-\sqrt{36}}{2}\\z_1=-\frac{6}{2}\\z_1=-3

Je calcule z_2=\frac{-b+\sqrt{\Delta}}{2a} en remplaçant a,b,\Delta  par 1,0,36.

z_2=\frac{-0+\sqrt{36}}{2\times 1}\\z_2=\frac{\sqrt{36}}{2}\\z_2=\frac{6}{2}\\z_2=3

Je conclus S=\{-3;3\}

Résolution de l’équation  par le calcul méthode n°2 ( beaucoup plus rapide).

z^2=9\\z^2=3^2

Si les carrés de deux nombres sont égaux, les nombres sont soit opposés, soit égaux.

z=-3 ou z=3

Je conclus S=\{-3;3\}

 2. Vérification à l’aide de Géogébra 

3. Vérification à l’aide de la TI 83 Premium CE ( on peut utiliser la calculatrice car tous les coefficients sont réels ).

Au clavier

A l’écran

Appuyer sur la touche resol du clavier, sélectionner 2: PlySmlt2 dans le menu déroulant, valider par entrer puis sélectionner 1: RACINES D’UN POLYNOME valider par entrer. Sélectionner le degré du polynôme, ici 2. Sélectionner a+bi. 

Appuyer sur la touche graph du clavier ( située sous SUIV de l’écran ), saisir l’équation. Attention, après avoir saisi le coefficient ou l’opération, toujours valider par entrer.   

Appuyer sur la touche graph ( située sous RESOL de l’écran ) clavier, les solutions apparaissent.

On veut résoudre l’équation  z^2=6z-9 ou z^2-6z+9=0.

 1. Résolution de l’équation  par le calcul.

J’identifie les coefficients l’équation a=1, b=-6 et c=9.

Je calcule \Delta=b²-4ac en remplaçant a,b,c  par 1, (-6) ,9.

\Delta=(-6)²-4\times{1}\times{9}\\\Delta=36-36\\\Delta=0

comme \Delta=0 , l’équation admet une solution réelle unique z_0=\frac{-b}{2a}.

Je calcule z_0=\frac{-b}{2a}en remplaçant a,b  par 1,(-6).

z_0=\frac{-(-6)}{2\times1}\\z_0=\frac{6}{2}\\z_0=3

 2. Vérification à l’aide de Géogébra 

3. Vérification à l’aide de la TI 83 Premium CE ( on peut utiliser la calculatrice car tous les coefficients sont réels ).

Au clavier

A l’écran

Appuyer sur la touche resol du clavier, sélectionner 2: PlySmlt2 dans le menu déroulant, valider par entrer puis sélectionner 1: RACINES D’UN POLYNOME valider par entrer. Sélectionner le degré du polynôme, ici 2. Sélectionner a+bi. 

Appuyer sur la touche graph du clavier ( située sous SUIV de l’écran ), saisir l’équation. Attention, après avoir saisi le coefficient ou l’opération, toujours valider par entrer.   

Appuyer sur la touche graph ( située sous RESOL de l’écran ) clavier, les solutions apparaissent.

On veut résoudre l’équation  4z^2+9=0.

 1. Résolution de l’équation  par le calcul méthode n°1 (celle vue dans l’exemple).

C’est une équation du second degré d’inconnue z.

J’identifie les coefficients l’équation a=4, b=0 et c=9.

Je calcule \Delta=b²-4ac  en remplaçant a,b,c  par 4, 0 ,9.

\Delta=0²-4\times{4}\times{9}\\\Delta=0-144\\\Delta=-144

comme \Delta<0 , l’équation admet deux solutions complexes conjuguées z_1=\frac{-b-i\sqrt{-\Delta}}{2a} et z_2=\overline{z_1}=\frac{-b+i\sqrt{-\Delta}}{2a}

Je calcule z_1=\frac{-b-i\sqrt{-\Delta}}{2a} en remplaçant a,b,\Delta  par 4,0,(-144).

z_1=\frac{-0-i\sqrt{-(-144)}}{2\times 4}\\z_1=\frac{-i\sqrt{144}}{8}\\z_1=-\frac{12}{8}i\\z_1=-\frac{3}{2}i

Pour calculer z_2, on utilise z_2=\overline{z_1}.

z_2=\overline{z_1}=\frac{3}{2}i

Je conclus S=\{-\frac{3}{2}i;\frac{3}{2}i\}

Résolution de l’équation  par le calcul méthode n°2 ( plus rapide).

4z^2+9=0\\z^2=-\frac{9}{4}\\z^2=(-1)\times \frac{9}{4}\\z^2=i^2\times {(\frac{3}{2})^2}\\z^2=(\frac{3}{2}i)^2\\z=-\frac{3}{2}i ou z=\frac{3}{2}i

Je conclus S=\{-\frac{3}{2}i;\frac{3}{2}i\}

 2. Vérification à l’aide de Géogébra 

3. Vérification à l’aide de la TI 83 Premium CE ( on peut utiliser la calculatrice car tous les coefficients sont réels ).

Au clavier

A l’écran

Appuyer sur la touche resol du clavier, sélectionner 2: PlySmlt2 dans le menu déroulant, valider par entrer puis sélectionner 1: RACINES D’UN POLYNOME valider par entrer. Sélectionner le degré du polynôme, ici 2. Sélectionner a+bi. 

Appuyer sur la touche graph du clavier ( située sous SUIV de l’écran ), saisir l’équation. Attention, après avoir saisi le coefficient ou l’opération, toujours valider par entrer.   

Appuyer sur la touche graph ( située sous RESOL de l’écran ) clavier, les solutions apparaissent.

On veut résoudre l’équation  z^2+5=2z ou z^2-2z+5=0

 1. Résolution de l’équation  par le calcul.

C’est une équation du second degré d’inconnue z.

J’identifie les coefficients l’équation a=1, b=-2 et c=5.

Je calcule \Delta=b²-4ac  en remplaçant a,b,c  par 1, (-2) ,5.

\Delta=(-2)²-4\times{1}\times{5}\\\Delta=4-20\\\Delta=-16

comme \Delta<0 , l’équation admet deux solutions complexes conjuguées z_1=\frac{-b-i\sqrt{-\Delta}}{2a} et z_2=\overline{z_1}=\frac{-b+i\sqrt{-\Delta}}{2a}

Je calcule z_1=\frac{-b-i\sqrt{-\Delta}}{2a} en remplaçant a,b,\Delta  par 1,(-2),(-16).

z_1=\frac{-(-2)-i\sqrt{-(-16)}}{2\times 1}\\z_1=\frac{2-i\sqrt{16}}{2}\\z_1=\frac{2-4i}{2}\\z_1=1-2i

Pour calculer z_2, on utilise z_2=\overline{z_1}.

z_2=\overline{z_1}=1+2i

Je conclus S=\{1-2i;1+2i\}

 2. Vérification à l’aide de Géogébra 

3. Vérification à l’aide de la TI 83 Premium CE ( on peut utiliser la calculatrice car tous les coefficients sont réels ).

Au clavier

A l’écran

Appuyer sur la touche resol du clavier, sélectionner 2: PlySmlt2 dans le menu déroulant, valider par entrer puis sélectionner 1: RACINES D’UN POLYNOME valider par entrer. Sélectionner le degré du polynôme, ici 2. Sélectionner a+bi. 

Appuyer sur la touche graph du clavier ( située sous SUIV de l’écran ), saisir l’équation. Attention, après avoir saisi le coefficient ou l’opération, toujours valider par entrer.   

Appuyer sur la touche graph ( située sous RESOL de l’écran ) clavier, les solutions apparaissent.

On remplace tous les z par 2 dans z^3-6z^2+16z-16=0 on s’assure que l’égalité est vérifiée.

2^3-6\times2^2+16\times 2-16=8-6\times4+32-16\\\hspace{4cm}=8-24+32-16\\\hspace{4cm}=0

Donc 2 est une solution de l’équation.

Déterminer a,b,c tels que z^3-6z^2+16z-16=(z-2)(az^2+bz+c)

On écrit l’égalité dans l’autre sens.

(z-2)(az^2+bz+c)=z^3-6z^2+16z-16

On développe le membre de gauche.

az^3+bz^2+cz-2az^2-2bz-2c=z^3-6z^2+16z-16

On ordonne le membre de gauche suivant les puissances décroissantes.

az^3+(b-2a)z^2+z(c-2b)-2c=z^3-6z^2+16z-16

On identifie les coefficients.

Les coefficients de z^3 sont égaux :a=1

Les coefficients de z^2 sont égaux :b-2a=-6

Les coefficients de z sont égaux :c-2b=16

Les coefficients constants sont égaux :-2c=-16 

On résout le système :

Donc z^3-2z^2+z-2=(z-2)(1\times z^2-4 z+8)

Ou z^3-2z^2+z-2=(z-2)( z^2-4z+8)

 

On veut résoudre l’équation (z-2)(z^2-4z+8)=0

On résout l’équation par le calcul en appliquant la règle du produit nul.

Le premier facteur est nul

z-2=0

C’est une équation du premier degré, on remet les membres à leur place.

z=2

Le second facteur est nul

z^2-4z+8=0

C’est une équation du second degré.

J’identifie les coefficients l’équation a=1, b=-4 et c=8.

Je calcule \Delta=b²-4ac  en remplaçant a,b,c  par 1,(-4) ,8.

\Delta=(-4)²-4\times{1}\times{8}\\\Delta=16-32\\\Delta=-16

comme \Delta<0 , l’équation admet deux solutions complexes conjuguées z_1=\frac{-b-i\sqrt{-\Delta}}{2a} et z_2=\overline{z_1}=\frac{-b+i\sqrt{-\Delta}}{2a}

Je calcule z_1=\frac{-b-i\sqrt{-\Delta}}{2a} en remplaçant a,b,\Delta  par 1,(-4),(-16).

z_1=\frac{-(-4)-i\sqrt{-(-16)}}{2\times 1}\\z_1=\frac{4-i\sqrt{16}}{2}\\z_1=\frac{4-4i}{2}\\z_1=2-2i

Pour calculer z_2, on utilise z_2=\overline{z_1}.

z_2=\overline{z_1}=2+2i

L’ensemble solution est  S=\{2;2-2i;2+2i\}

On applique la règle du produit nul.

On vérifie les résultats obtenus avec Géogébra.

 

 

 

Réponse:

\overrightarrow{DC}=\overrightarrow{HG}.

Résoudre graphiquement f(x)=1

C’est une autre façon de demander de déterminer graphiquement les antécédents de 1.

Je place 1 sur l’axe des ordonnées, je trace alors la parallèle à l’axe des abscisses passant par 1 toute entière. Je repère les points d’intersection avec la courbe. Les abscisses de ces points sont les antécédents de 1.

Les antécédents sont -2 et 2.

Donc S=\{-2;2\}

Remarque : comme on demande de résoudre une équation, il faut écrire ainsi l’ensemble des solutions.