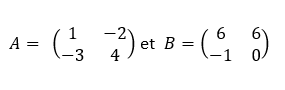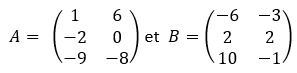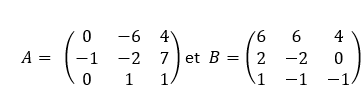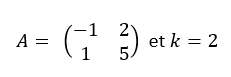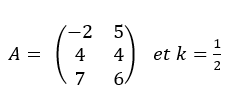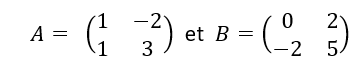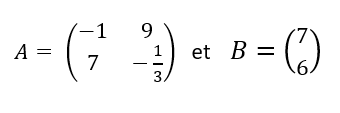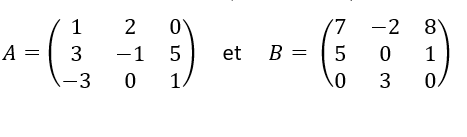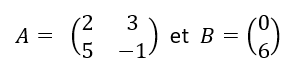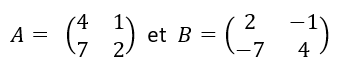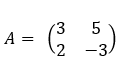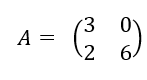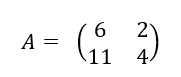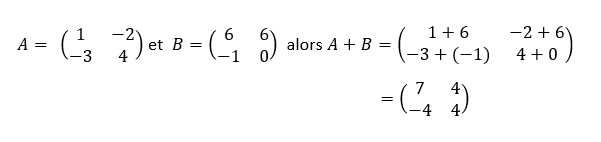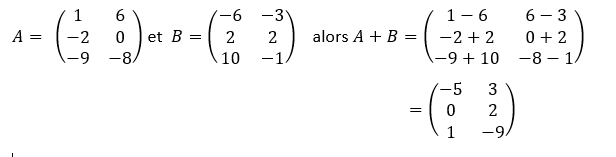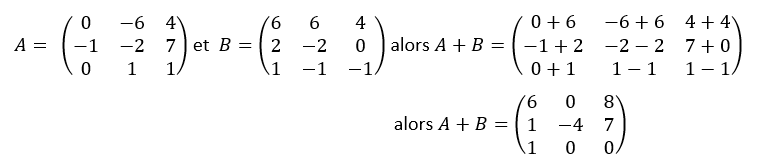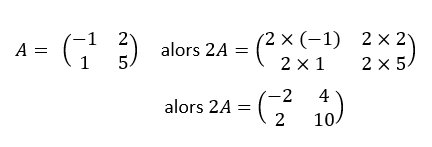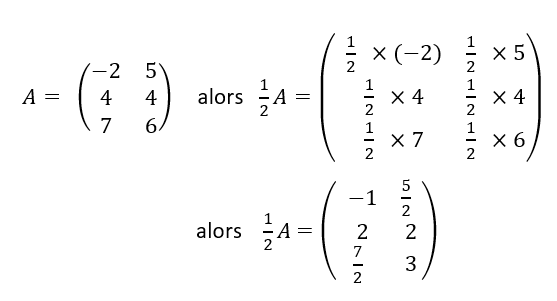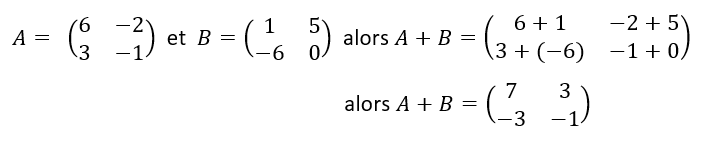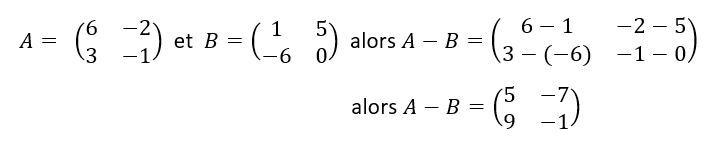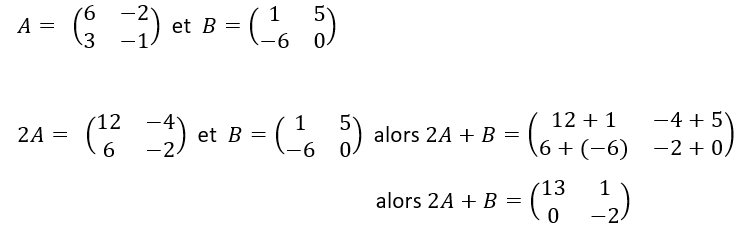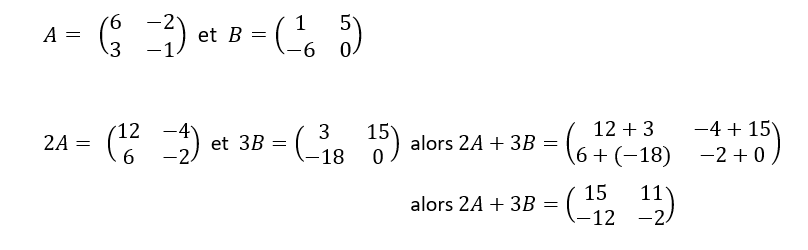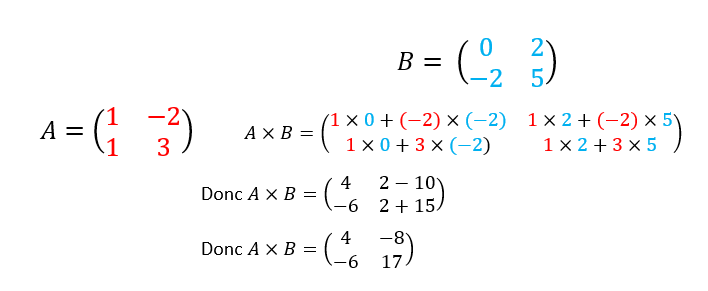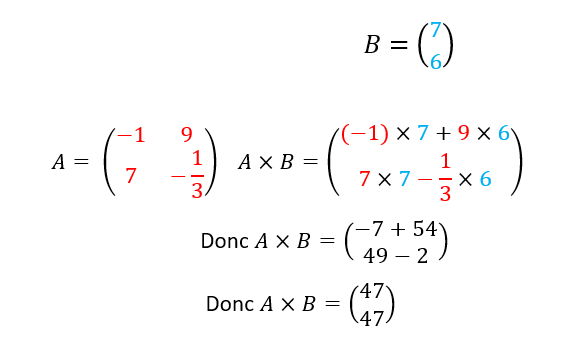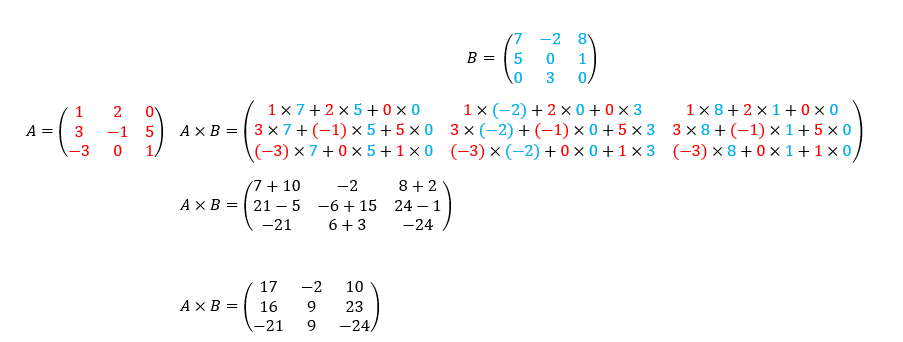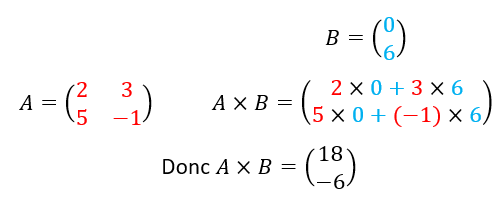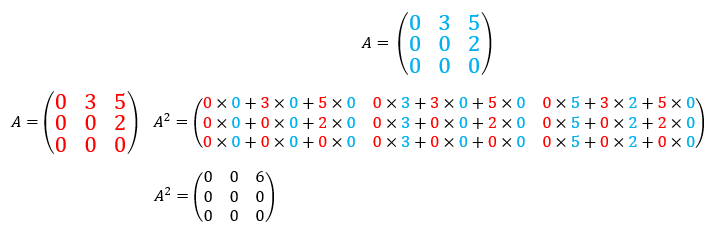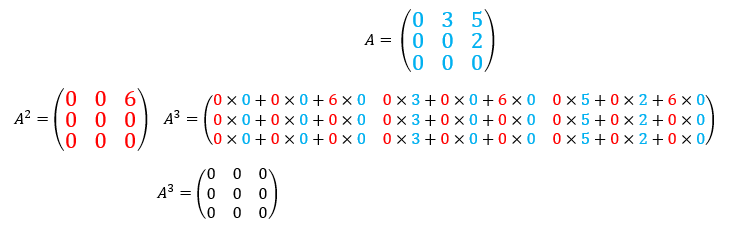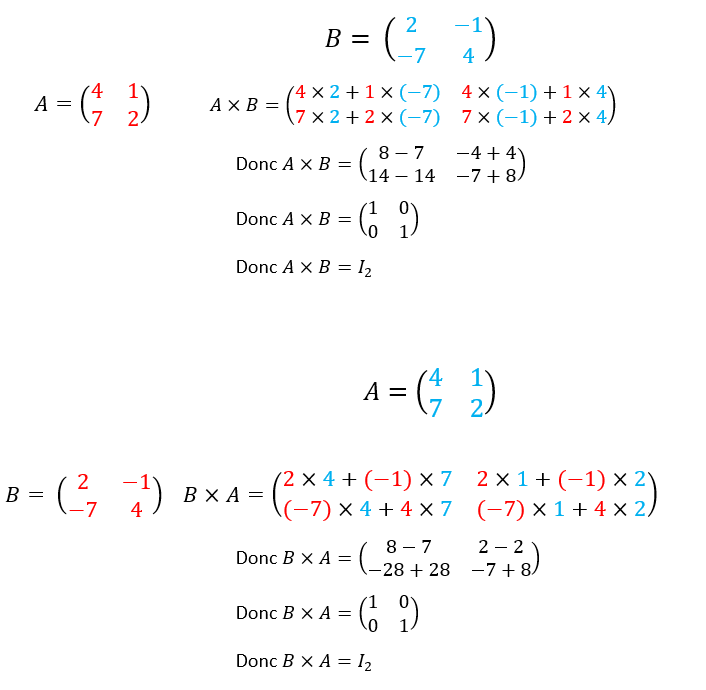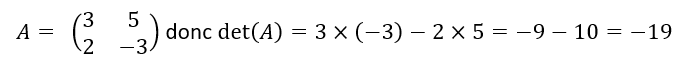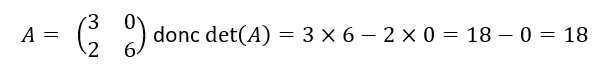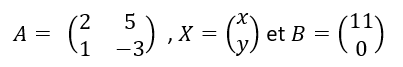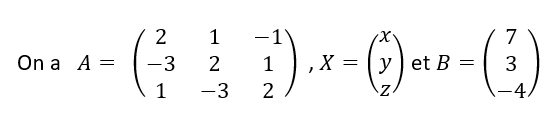Sommaire
Notion de matrices
Définition
Une matrice de taille n\times p est un tableau de nombres réels à n lignes et p colonnes.
Le nombre réel situé sur la ième ligne et la jème colonne est noté a_{ij}
Exemples
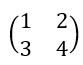
est une matrice de taille 2\times 2 avec a_{11}=1 , a_{12}=2 , a_{21}=3 et a_{22}=4.
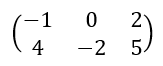
est une matrice de taille 2\times 3 avec a_{11}=-1 , a_{12}=0 , a_{13}=2 , a_{21}=4 , a_{22}=-2 et a_{23}=5.
Définir une matrice avec la TI 83 Premium CE
Au clavier
A l’écran
On tape sur la touche matrice puis on sélectionne la colonne EDIT et on sélectionne la ligne 1:[A].
Compléter en indiquant le nombre de ligne et le nombre de colonnes.
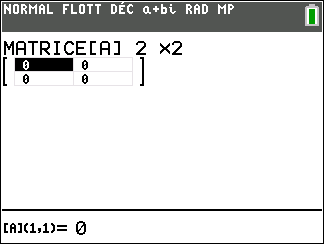
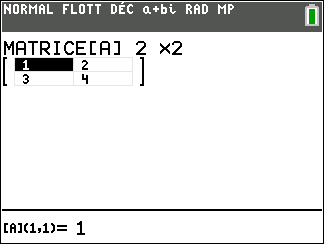
On complète les cadres avec les coefficients de la matrice en validant par entrer.
La matrice [A] est alors enregistrée une bonne fois pour toutes.
Supprimer une matrice avec la TI 83 Premium CE
Pour supprimer une matrice, appuyer sur la touche mém (c’est-à-dire 2nde et +). Sélectionner 2:Gest.Mémoite/Suppr, valider par entrer .Puis choisissez 5: Matrice, valider par entrer. Reste à sélectionner ce que vous souhaitez voir disparaître et pour chaque matrice appuyez sur la touche suppr.
Pour supprimer une matrice, appuyer sur la touche mém (c’est-à-dire 2nde et +). Sélectionner 2:Gest.Mémoite/Suppr, valider par entrer .Puis choisissez 5: Matrice, valider par entrer. On sélectionne par exemple la matrice [A] avec entrer.
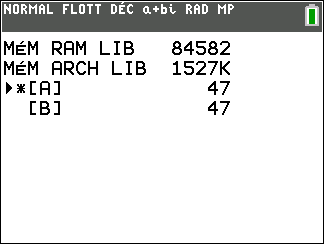
On appuie ensuite sur la touche suppr (si besoin est on répond 2:oui à la question : En êtes vous sûr ? On valide avec entrer).
Définition
Si n=1 , il n’y a qu’une ligne. On dit que c’est une matrice ligne.
Si p=1 , il n’y a qu’une colonne. On dit que c’est une matrice colonne.
Si n=p , il y a autant de lignes que de colonnes. On dit que c’est une matrice carrée d’ordre n.
Une matrice diagonale est une matrice dont tous les cofficients sont nuls sauf les coefficients pour lesquels i=j.
La matrice identité d’ordre n est la matrice diagonale d’ordre n dont tous les cofficients sur la diagonale sont égaux à 1. On la note I_n.
La matrice nulle de taille n\times p est la matrice dont tous les coefficients sont nuls.
Exemples
est une matrice ligne avec a_{11}=-1 , a_{12}=0 , a_{13}=5.
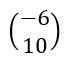
est une matrice colonne avec a_{11}=-6 , a_{21}=10.
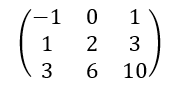
est une matrice carrée d’ordre 3 avec a_{11}=-1 , a_{12}=0 , a_{13}=1 , a_{21}=1 , a_{22}=2 , a_{23}=3 , a_{31}=3 , a_{32}=6 et a_{33}=10.

est la matrice nulle d’ordre 3 avec a_{11}=0 , a_{12}=0 , a_{13}=0 , a_{21}=0 , a_{22}=0 , a_{23}=0 , a_{31}=0 , a_{32}=0 et a_{33}=0.
Addition de deux matrices
définition
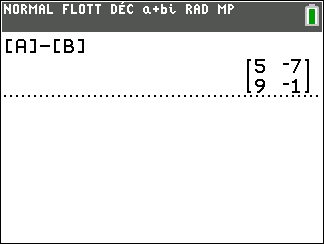
L’addition de deux matrices de même format se fait en ajoutant les nombres situés au même endroit dans les deux matrices
Exemple
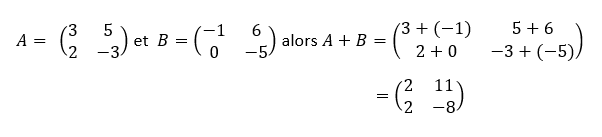
Ajouter deux matrices avec la TI 83 Premium CE
Au clavier
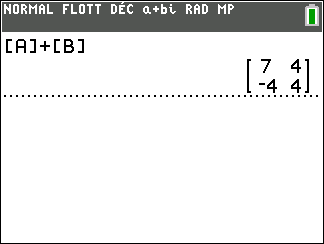
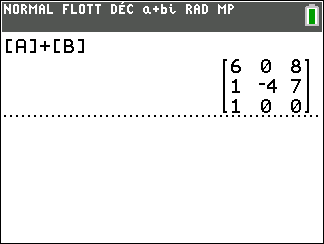
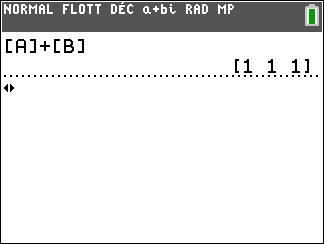
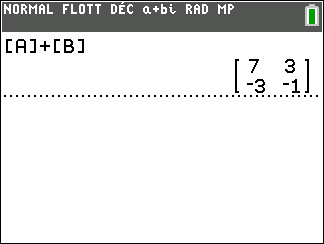
A l’écran
On a d’abord défini les deux matrices [A] et [B] à l’aide de la calculatrice.
On tape sur la touche matrice puis on sélectionne la colonne NOMS et on sélectionne la ligne 1:[A] et on valide par entrer.
On tape sur la touche + de la calculatrice.
Puis on tape sur la touche matrice , on sélectionne la colonne NOMS et on sélectionne la ligne 2:[B] et on valide par entrer.
On refait entrer pour ajouter.
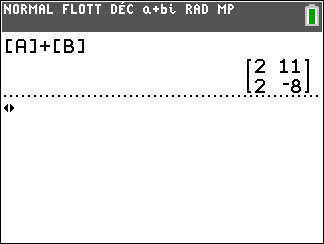
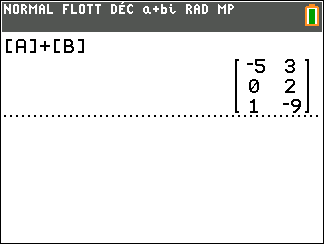
Exercice n°1 :
Ajouter les matrices A et B.
Produit d’une matrice par un réel
définition
On multiplie une matrice par un nombre réel en multipliant tous les coefficients de la matrice par ce nombre réel.
Exemple
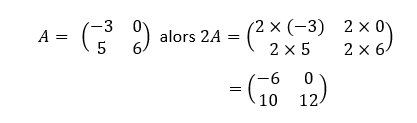
Multiplier une matrice par un nombre réel avec la TI 83 Premium CE
Au clavier
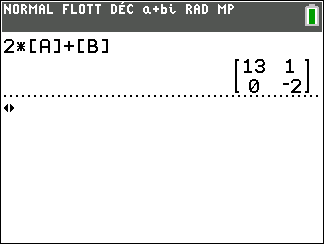
A l’écran
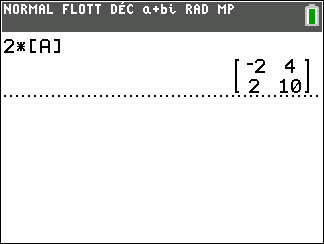
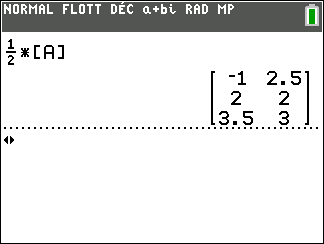
On a d’abord défini la matrice [A] à l’aide de la calculatrice.
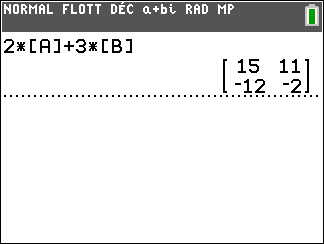
On tape sur la touche 2 puis sur la touche multiplication x. Ensuite on tape sur la touche matrice puis on sélectionne la colonne NOMS et on sélectionne la ligne 1:[A] et on valide par entrer. On refait entrer.
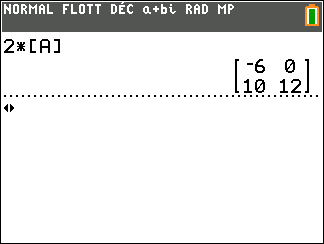
Exercice n°2 :
Effectuer le produit du réel k par la matrice A.
Exercice n°3 :
On considère les matrices suivantes :
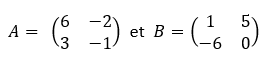
Effectuer les opérations suivantes.
Produit de matrices
définition
Pour effectuer le produit A\times B il faut que le nombre de colonnes de la matrice A soit égal au nombre de lignes de la matrice B.
Le coefficient de la matrice produit situé à la ième ligne et à la jème colonne est le produit de la ième ligne de A par la jème ligne de B.
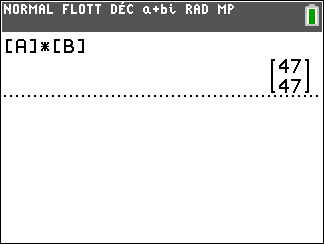
Exemple
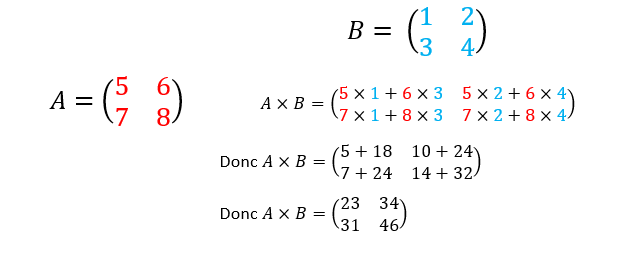
Multiplier deux matrices avec la TI 83 Premium CE
Au clavier
A l’écran
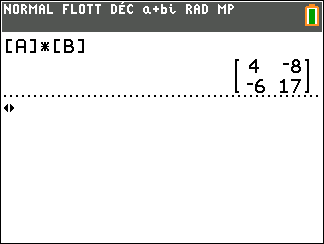
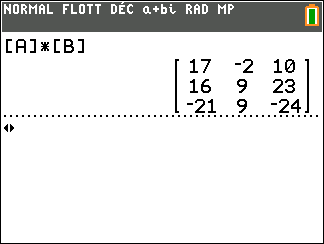
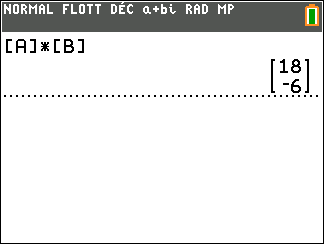
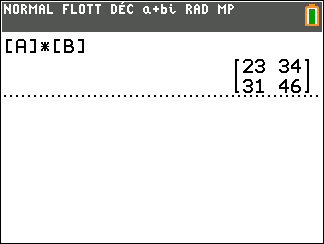
On a d’abord défini les deux matrices [A] et [B] à l’aide de la calculatrice.
On tape sur la touche matrice puis on sélectionne la colonne NOMS et on sélectionne la ligne 1:[A] et on valide par entrer.

On tape sur la touche multiplier \times de la calculatrice.
Puis on tape sur la touche matrice , on sélectionne la colonne NOMS et on sélectionne la ligne 2:[B] et on valide par entrer.
On refait entrer pour ajouter.
Exercice n°4
Multiplier les matrices A et B. Les matrices proposées sont telles que le nombre de colonnes de la matrice A est égal au nombre de lignes de la matrice B.
Puissance d’une matrice
définition
Pour tout entier naturel n non nul, on définit la puissance nième d’un matrice A notée A^n par A^n=A\times A\times…\times A (n fois).
De plus A^0=1.
Exemple
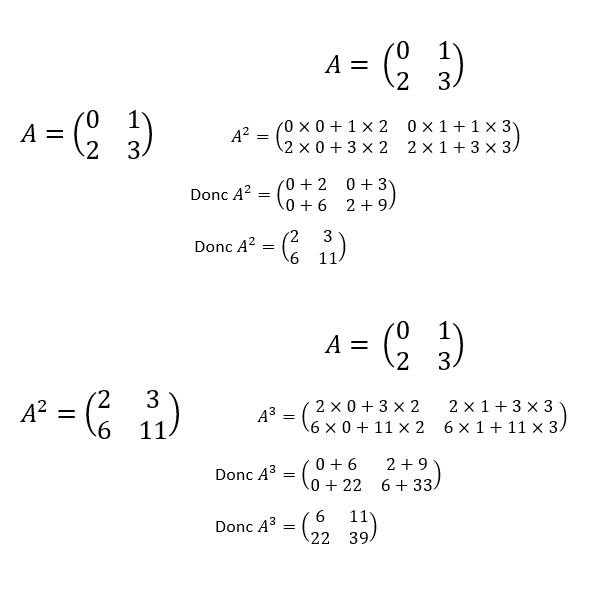
Calculer la puissance d’une matrice avec la TI 83 Premium CE
Au clavier
A l’écran
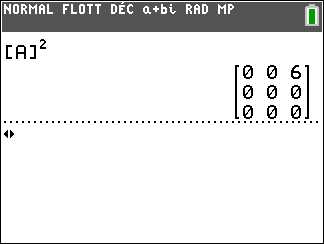
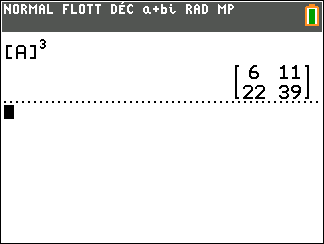
On a d’abord défini la matrice [A] à l’aide de la calculatrice.
On tape sur la touche matrice puis on sélectionne la colonne NOMS et on sélectionne la ligne 1:[A] et on valide par entrer.

On tape sur la touche puissance ^ de la calculatrice.
Puis on tape 3 on valide par entrer.
Exercice n°5 :
On considère la matrice :
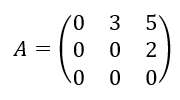
- Calculer A^2.
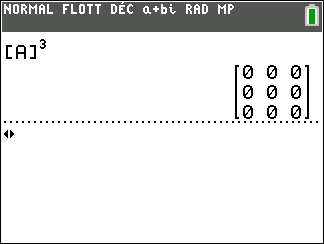
2. Calculer A^3.
Matrice inverse d’une matrice carrée
définition
Une matrice A de taille n est inversible lorsqu’il existe une matrice B de taille n telle que
A\times B=B\times A =I_n.
En général l’inverse de A est notée A^{-1}.
Exemple
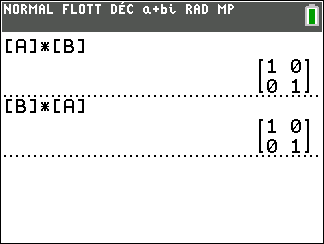
Montrons que les matrices suivantes sont inverses l’une de l’autre.
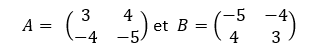
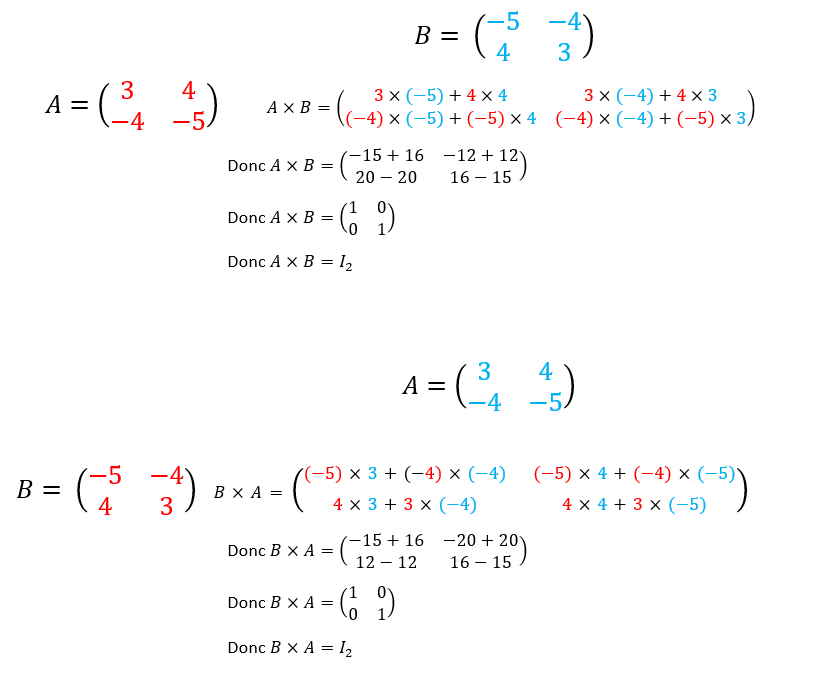
Exercice n°6 :
Montrons que les matrices suivantes sont inverses l’une de l’autre.
définition
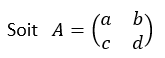
Le déterminant de A est le réel, noté det(A) défini par
det(A)=ad-bc.
Calculer le déterminant d’une matrice avec la TI 83 Premium CE
Au clavier
A l’écran
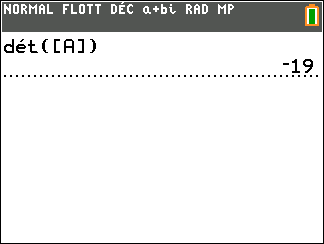
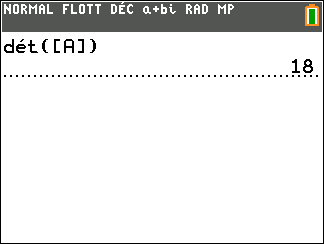
On a d’abord défini la matrice [A] à l’aide de la calculatrice.
On tape sur la touche matrice puis on sélectionne la colonne MATH et on sélectionne la ligne 1:det et on valide par entrer. Puis on tape sur la touche matrice puis on sélectionne la colonne NOMS et on sélectionne la ligne 1:[A] et on valide par entrer.
Exercice n°7 :
Calculer les déterminants des matrices carrées d’ordre 2 suivantes :
propriété
Une matrice carrée est inversible si et seulement si son déterminant est non nul.

Exemple
Déterminer si c’est possible la matrice inverse de A notée A^{-1}.
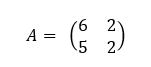
On calcule d’abord det(A)=ad-bc
det(A)=6\times 2-5\times2=12-10=2.
Comme det(A)\ne 0, la matrice A est inversible. On applique la propriété précédente.
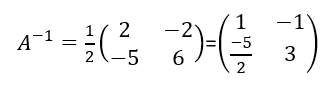
Calculer l’inverse d’une matrice avec la TI 83 Premium CE
Au clavier
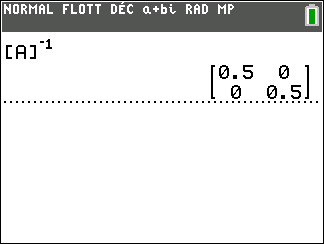
A l’écran
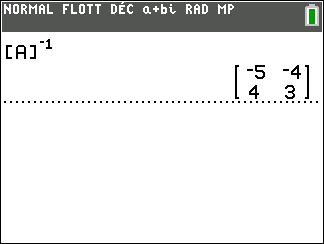
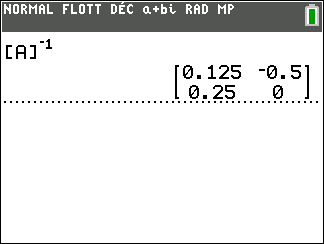
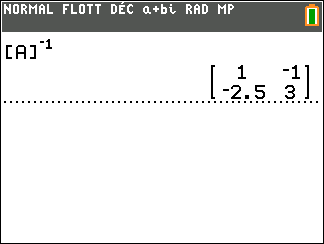
On a d’abord défini la matrice [A] à l’aide de la calculatrice.
On tape sur la touche matrice puis on sélectionne la colonne NOMS et on sélectionne la ligne 1:[A] et on valide par entrer.

On tape sur la touche 2nde puis sur la touche matrice de la calculatrice. On valide avec entrer.
Exercice n°8 :
Calculer les déterminants des matrices carrées d’ordre 2 suivantes :
propriété
Soit A une matrice carrée d’ordre n et X et B deux matrices colonnes à n lignes.
Si A est inversible, alors le système d’écriture matricielle AX=B admet une unique solution donnée par la matrice colonne X=A^{-1}\times B .
Exemple
On veut résoudre le système suivant :
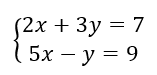
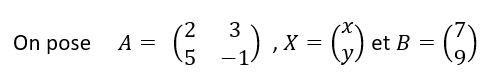
Le système peut s’écrire AX=B .
On calcule det(A)=2\times (-1)-3\times5=-2-15=-17, donc la matrice A est inversible et donc l’équation AX=B admet une solution X=A^{-1}\times B .
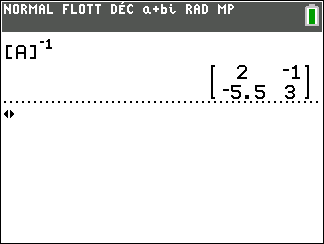
Calculons A^{-1} .
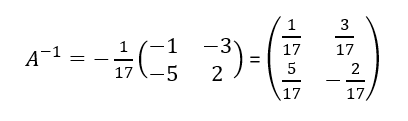
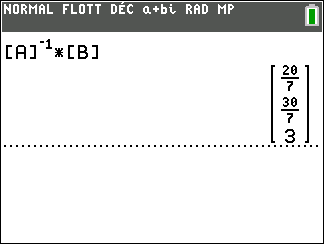
Calculons A^{-1}\times B .

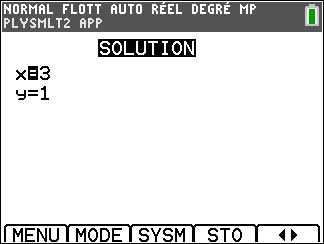
Donc le système a pour solution le couple (2;1).
Exercice n°9 :
On considère le système suivant :
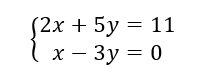
- Déterminer A , Xet B pour que le système puisse s’écrire AX=B .
2. Calculer A{-1}\times B et en déduire le couple-solution du système.
Exercice n°10 :
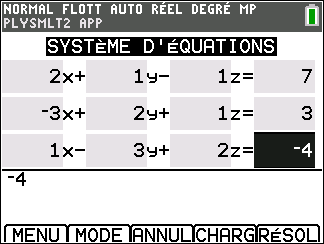
On considère le système suivant :
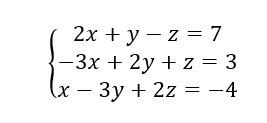
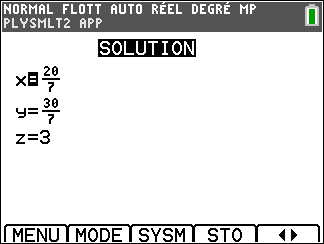
- Déterminer A , Xet B pour que le système puisse s’écrire AX=B .
2. Calculer A{-1}\times B à l’aide de la calculatrice et en déduire le couple-solution du système.