Sommaire
Définitions
Un graphe est une représentation composée de sommets (des points) reliés par des arêtes (la plupart du temps des segments).
Un graphe orienté est un graphe dont les arêtes sont munies d’un sens de parcours.
L’ordre d’un graphe est le nombre de sommets de ce graphe.
Le degré d’un sommet est le nombre d’arêtes incidentes à ce sommet, sans tenir compte de leur éventuel sens de parcours.
Exemple
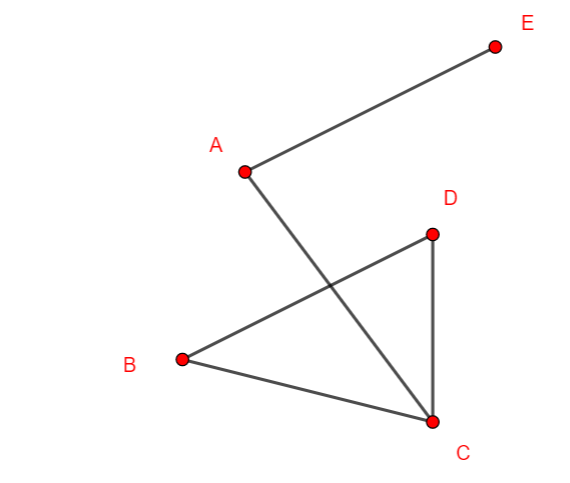
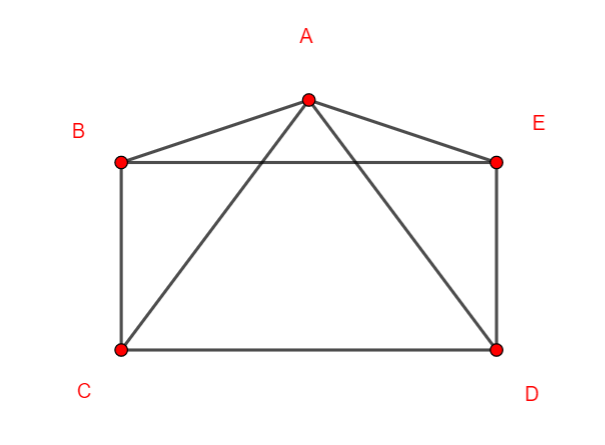
Le graphe ci-contre a 5 sommets, il est d’ordre 5.
Il a 5 arêtes.
Il n’est pas orienté.
Le sommet E est d’ordre 1, les sommets A, B et D sont d’ordre 2 et le sommet C est d’ordre 3.
Exercice n°1
Pour chaque graphe, donner son ordre et le degré de chaque sommet.
Définitions
Deux sommets sont adjacents lorsqu’ils sont reliés par au moins une arête.
Un graphe est complet lorsque tous ses sommets sont deux à deux adjacents.
Méthode
Un graphe est complet si chaque sommet est relié à tous les autres.
Exemple

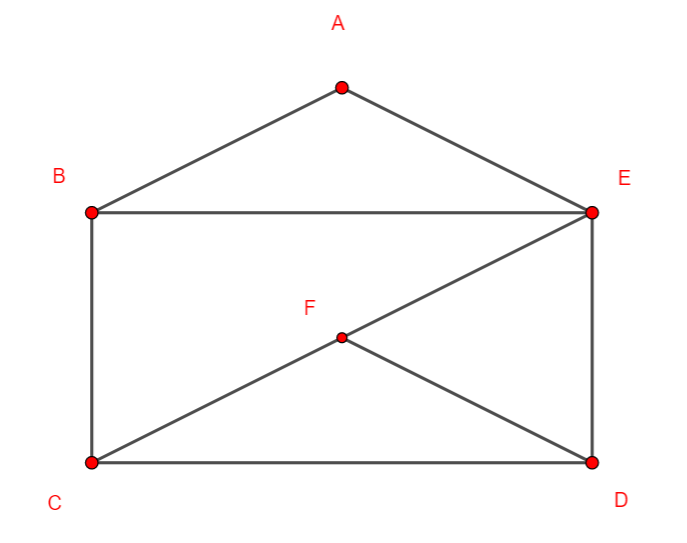
Le graphe ci-dessus n’est pas complet car, par exemple, les sommets E et D ne sont pas adjacents.
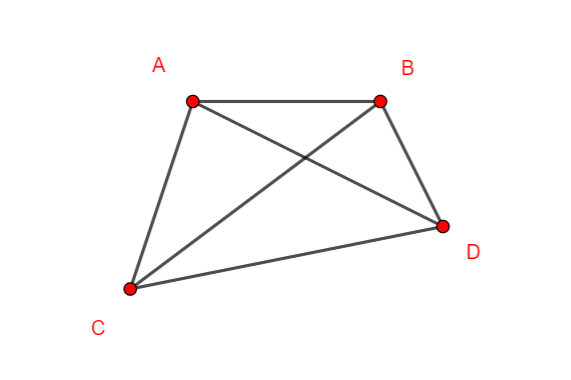
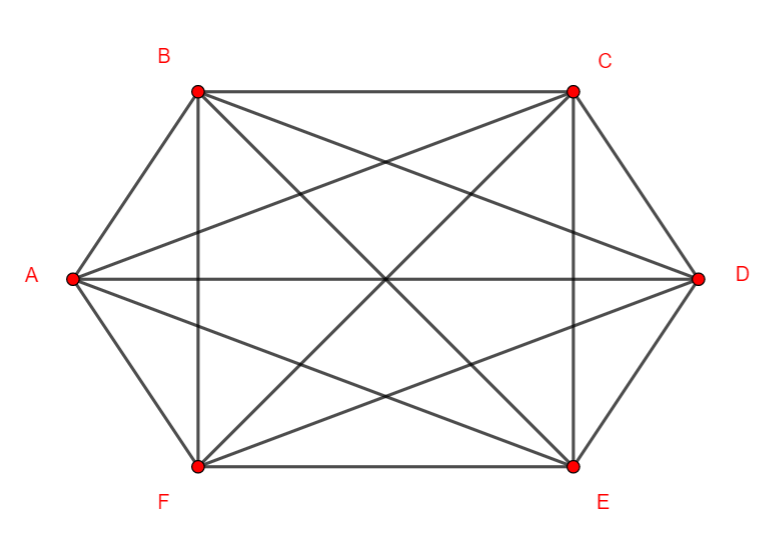
Le graphe ci-dessus est complet car tous ses sommets sont deux à deux adjacents.
C’est-à-dire que chaque sommet est relié à tous les autres.
Exercice n°2
On reprend les graphes de l’exercice n°1. Pour chaque graphe, dire s’il est complet ou pas.
Définitions
Pour un graphe non orienté, une chaîne est une suite d’arêtes consécutives reliant deux sommets (éventuellement confondus).
La longueur d’une chaîne est le nombre d’arêtes la composant.
Pour un graphe orienté, un chemin est une suite d’arêtes consécutives reliant deux sommets (éventuellement confondus) en tenant compte du sens de parcours des arêtes.
Exemples

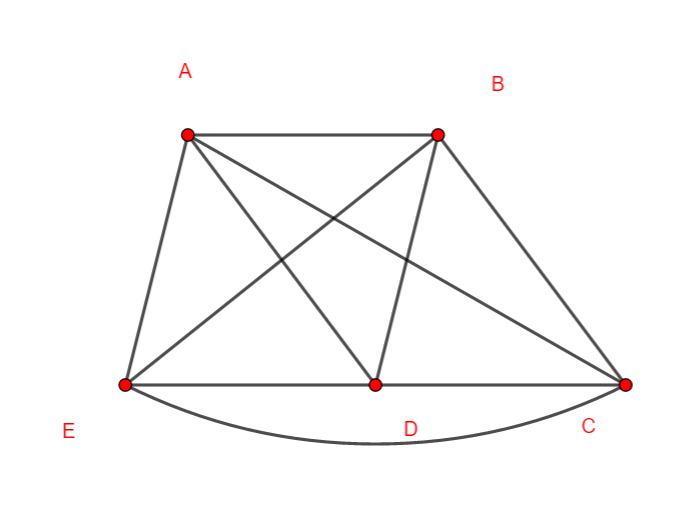
Sur le graphe ci-dessus E-A-C-D-B-C est une chaîne de longueur 5.

Sur le graphe ci-dessus C-A-B-D-C est une chaîne de longueur 4.
Définition
Un graphe est connexe lorsque chaque couple de ses sommets peut être relié par une chaîne.
Méthode
Le graphe est connexe si on peut trouver une chaîne qui passe par tous les sommets.
Exemples

Ce graphe ci-dessus est connexe car il existe une chaîne qui passe par tous les sommets du graphe.
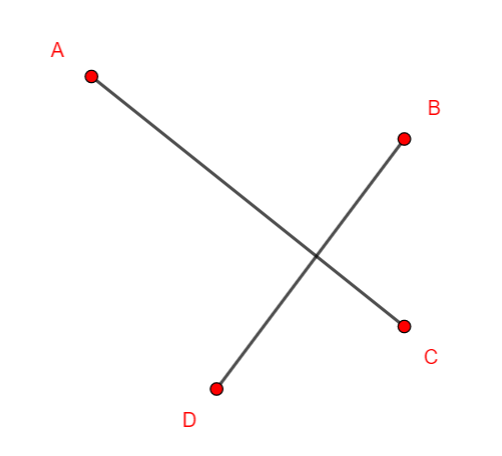
Le graphe ci-dessus n’est pas connexe car on ne peut pas relier A et B par une chaîne.
Exercice n°3
Pour chaque graphe, dire s’il est connexe ou pas.