Sommaire
Définition
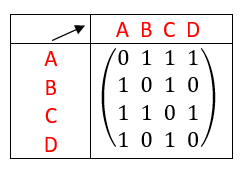
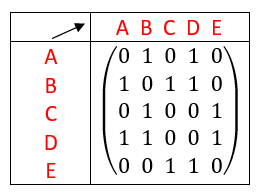
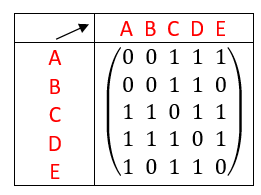
Soit n un entier naturel non nul. On considère un graphe d’ordre n (orienté ou non) dont les sommets sont numérotés de 1 à n et rangés dans l’ordre croissant.
La matrice d’adjacence de ce graphe est la matrice carrée d’ordre n, dont le coefficient a_{i,j} est le nombre d’arêtes partant du sommet i pour arriver au sommet j.
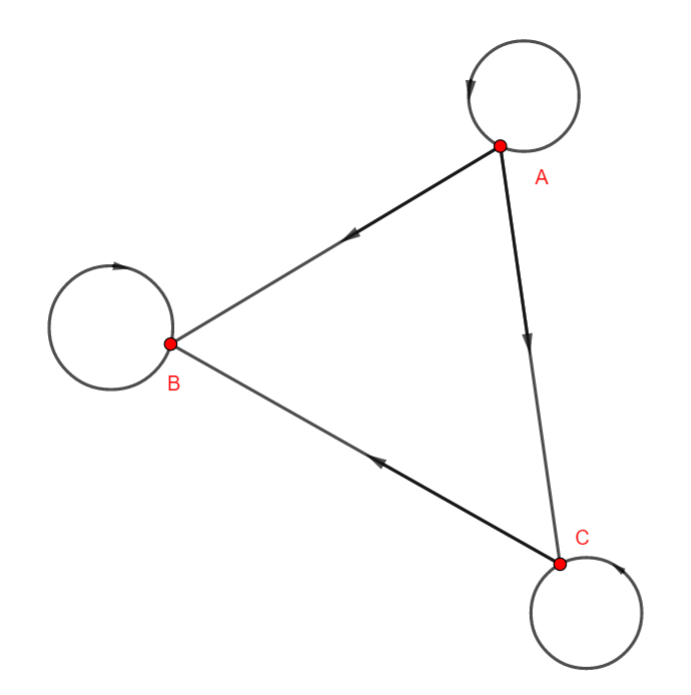
En rangeant les sommets dans l’ordre alphabétique, déterminer la matrice adjacente pour les graphes non orientés ci-dessous dans chaque cas.
Exemple n°1.1
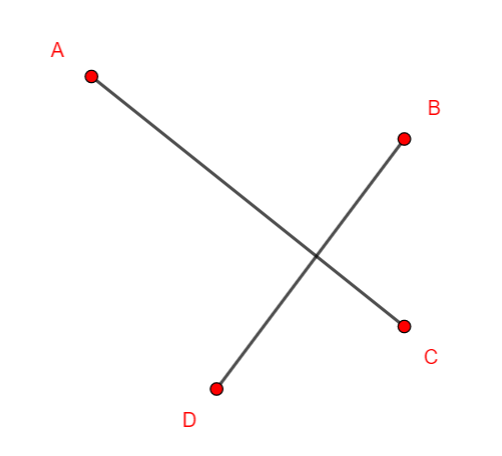
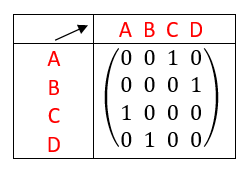
Exemple n°1.2
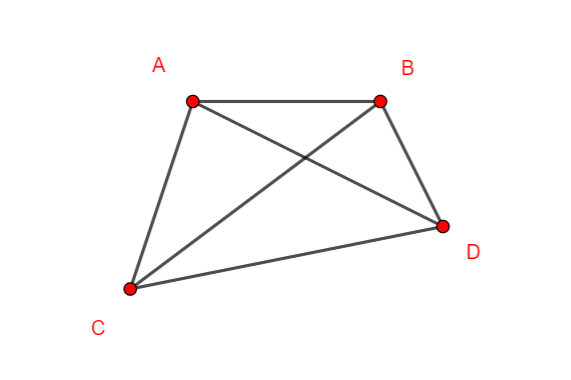
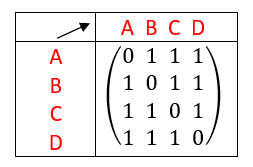
Exemple n°1.3
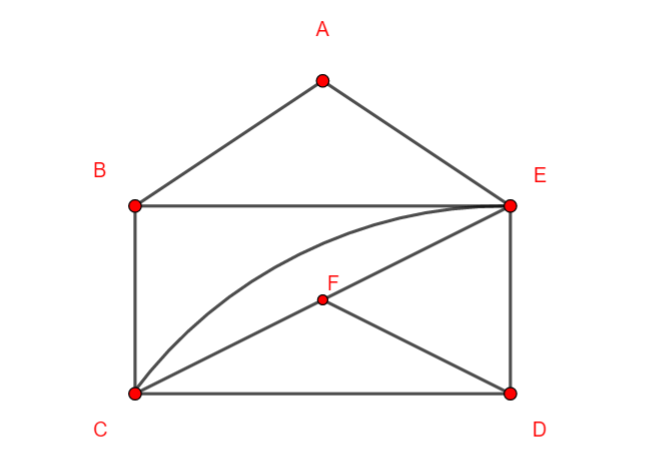
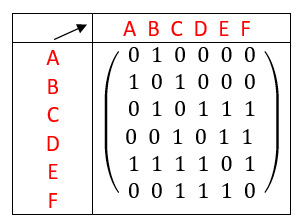
Exemple n°1.4 graphe orienté
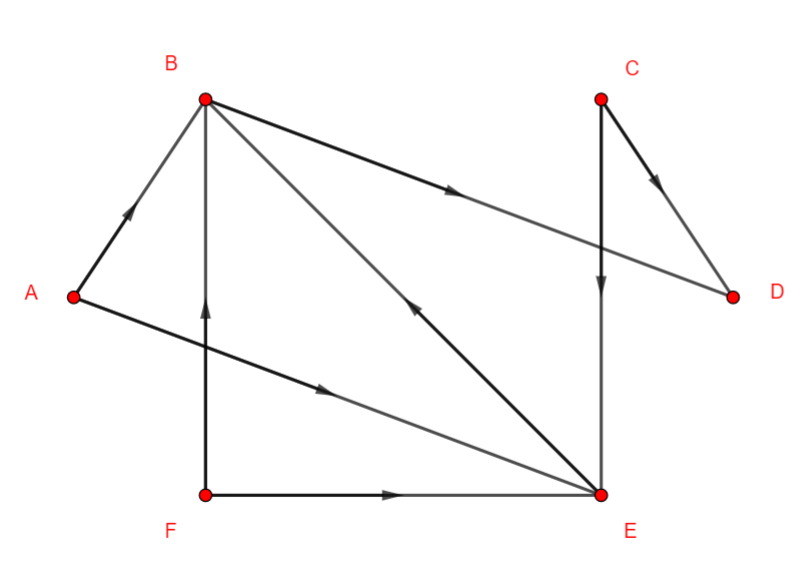
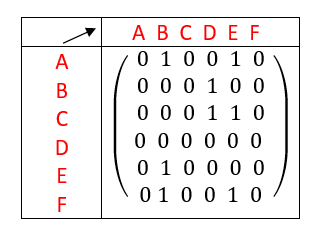
Exemple n°1.5 graphe orienté
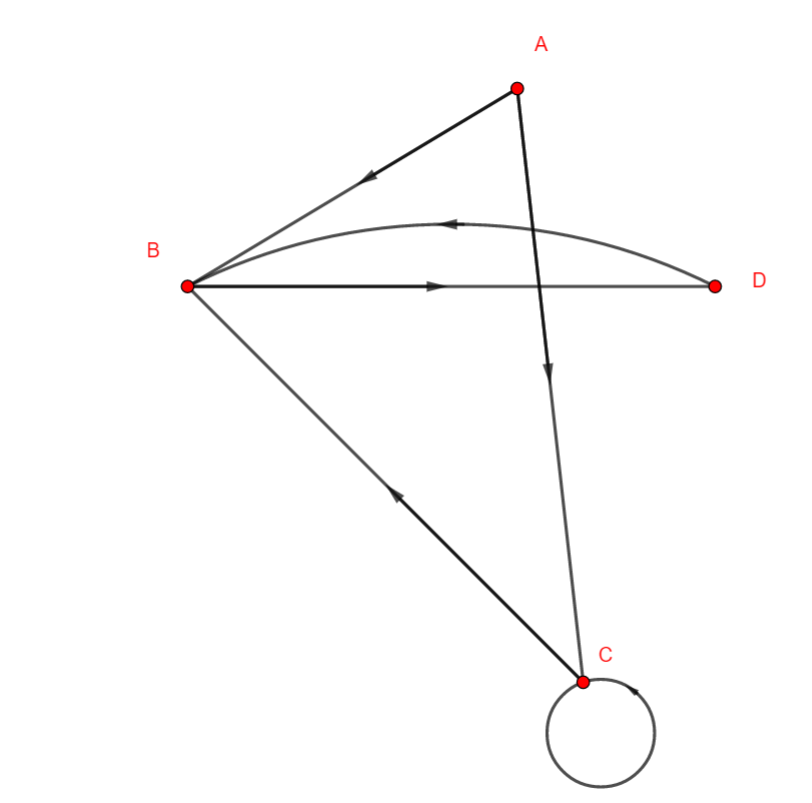
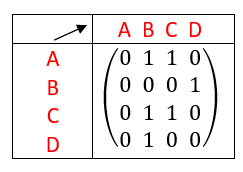
Exemple n°1.6 graphe orienté
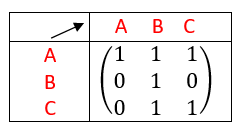
Propriétés
Soit n et k deux entiers naturels non nuls et M , la matrice d’adjacence d’un graphe d’ordre n dont les sommets sont numérotés de 1 à n et rangés dans l’ordre croissant.
Le terme de la i-ème ligne et de la j-ème colonne de la matrice M^k, dont le coefficient a_{i,j} donne le nombre de chaînes de longueur k qui relie le sommet i au sommet j.
On reprend les exemples précédents.
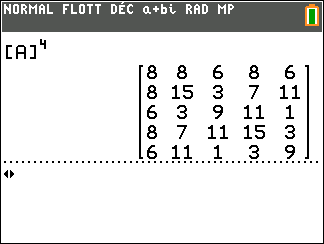
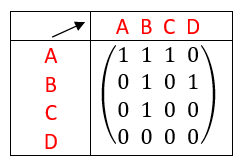
Exemple n°2.1


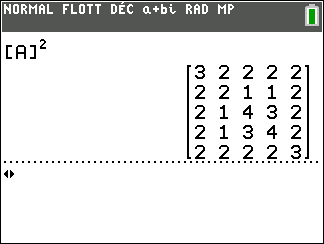
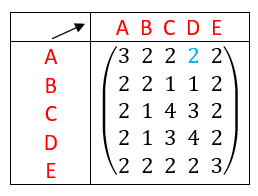
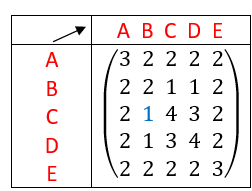
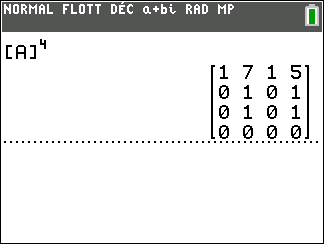
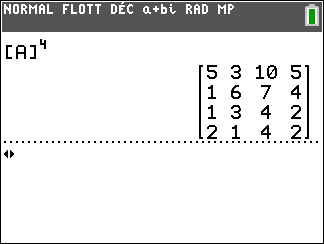
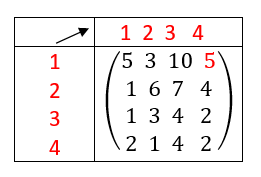
On calcule A^4 à l’aide de la calculatrice :
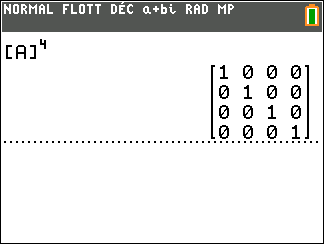
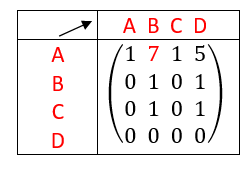
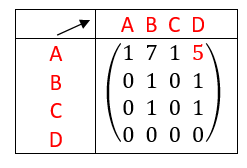
On interprète les coefficients de A^4 comme des nombres de chaînes reliant deux sommets.
Il existe une chaîne de longueur 4 qui relie le sommet A au sommet A. Idem pour les sommets B, C et D.
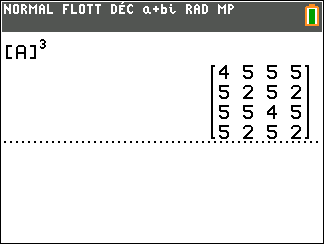
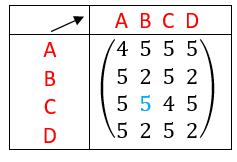
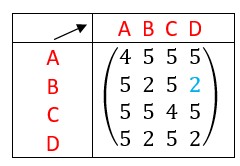
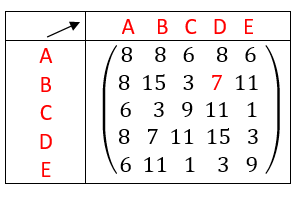
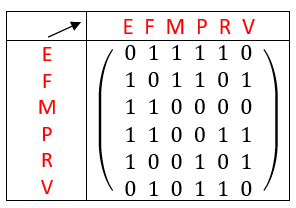
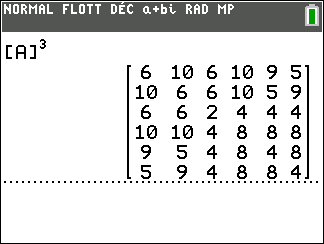
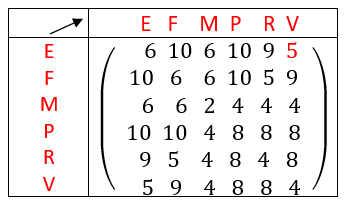
Exemple n°2.2


On calcule A^3 à l’aide de la calculatrice :
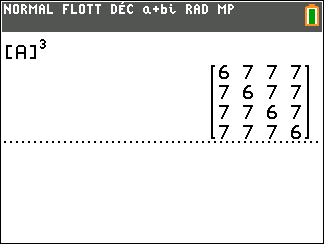
On interprète les coefficients de A^3 comme des nombres de chaînes reliant deux sommets.
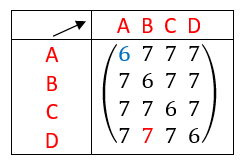
Il existe six chaînes de longueur 3 qui relient le sommet A au sommet A.
Il existe sept chaînes de longueur 3 qui relient le sommet D au sommet B.
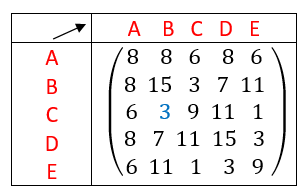
Exemple n°2.3


On calcule A^2 à l’aide de la calculatrice :
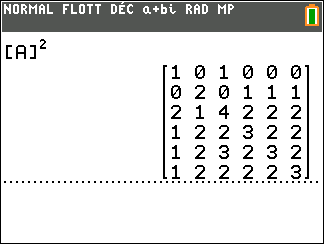
On interprète les coefficients de A^2 comme des nombres de chaînes reliant deux sommets.
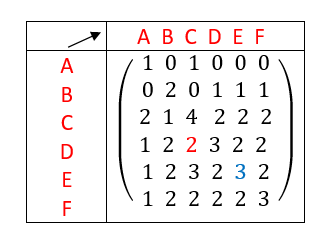
Il existe deux chaînes de longueur 2 qui relient le sommet D au sommet C.
Il existe trois chaînes de longueur 2 qui relient le sommet E au sommet E.
Exercice n°1
On considère le graphe non orienté suivant
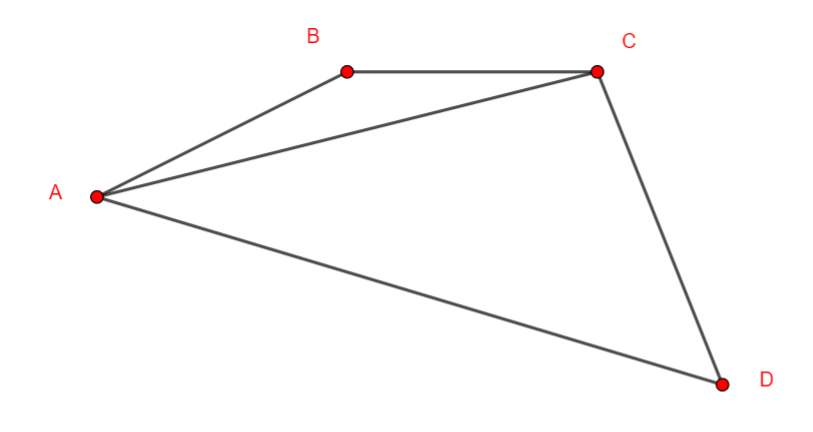
- Déterminer la matrice adjacente du graphe ci-dessus.
2.a. Déterminer le nombre de chaînes d’ordre 3 reliant le sommet C au sommet B.
2.b. Déterminer le nombre de chaînes d’ordre 3 reliant le sommet B au sommet D.
Exercice n°2
On considère le graphe non orienté suivant
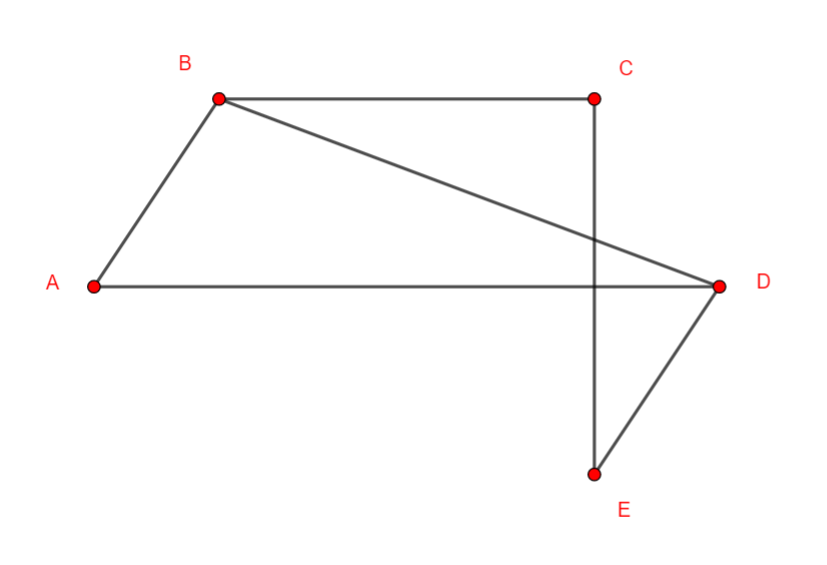
- Déterminer la matrice adjacente du graphe ci-dessus.
2.a. Déterminer le nombre de chaînes d’ordre 4 reliant le sommet C au sommet B.
2.b. Déterminer le nombre de chaînes d’ordre 4 reliant le sommet B au sommet D.
Exercice n°3
On considère le graphe non orienté suivant
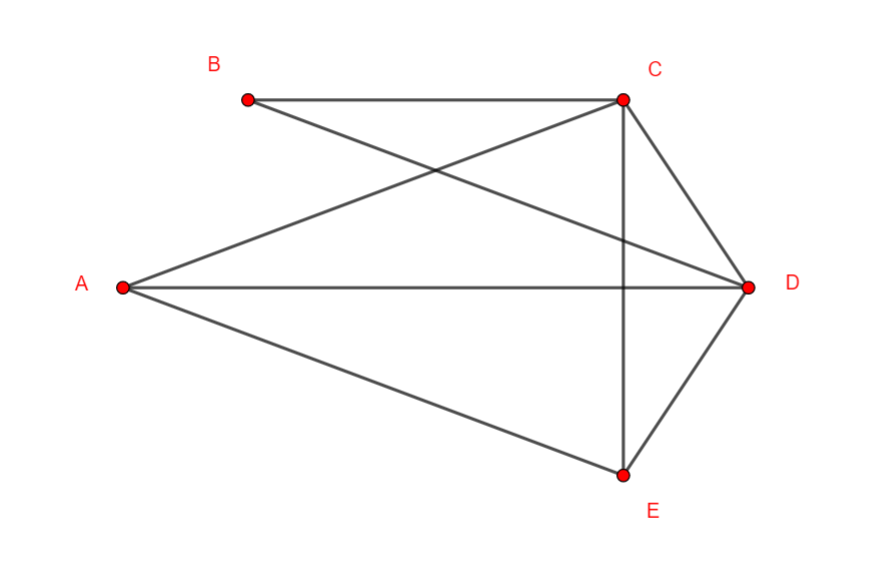
- Déterminer la matrice adjacente du graphe ci-dessus.
2.a. Déterminer le nombre de chaînes d’ordre 2 reliant le sommet A au sommet D.
2.b. Déterminer le nombre de chaînes d’ordre 2 reliant le sommet B au sommet D.
Exercice n°4
On considère le graphe orienté suivant
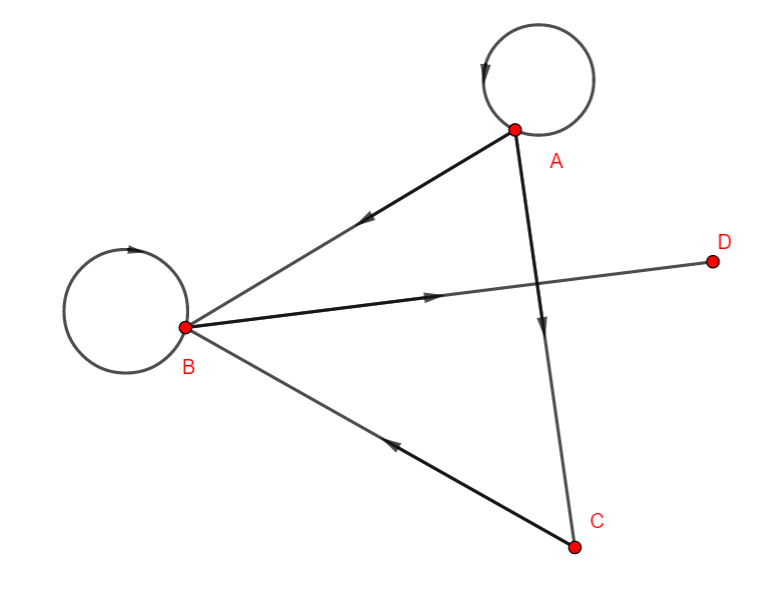
- Déterminer la matrice adjacente du graphe ci-dessus.
2.a. Déterminer le nombre de chaînes d’ordre 4 reliant le sommet A au sommet B.
2.b. Déterminer le nombre de chaînes d’ordre 4 reliant le sommet A au sommet D.
Exercice n°5 : D’après sujet Bac ES 2019 Centres étrangers
Un restaurateur se fournit auprès de 5 producteurs locaux. Le graphe ci-dessous représente la situation géographique du restaurateur et de ses fournisseurs, les arêtes correspondant au réseau routier et les sommets aux producteurs :
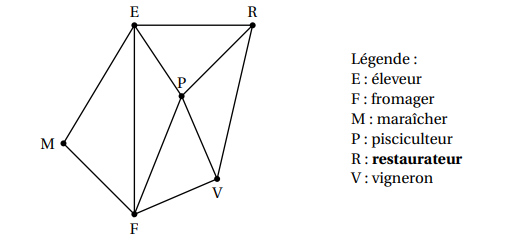
1. a. Le graphe est-il complet ? Justifier la réponse.
b. Le graphe est-il connexe ? Justifier la réponse.
2. On appelle N la matrice d’adjacence associée à ce graphe, les sommets étant pris dans l’ordre alphabétique.
a. Déterminer la matrice N.
b. Déterminer la matrice N^3 à l’aide de la calculatrice. En déduire le nombre de chemins de longueur 3 reliant l’éleveur au vigneron.
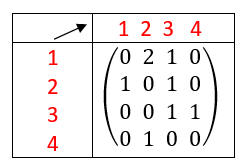
Exercice n°6 : D’après sujet Bac ES 2019 Amérique du Nord
Pour accéder à un local d’une petite entreprise, les employés doivent choisir un code reconnu par l’automate suivant :
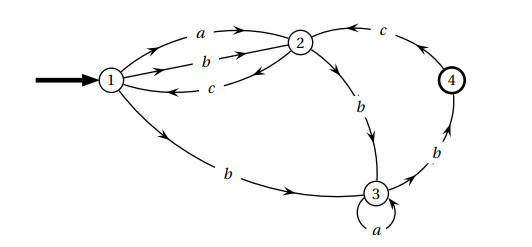
Une succession de lettres constitue un code possible si ces lettres se succèdent sur un chemin du
graphe orienté ci-dessus, en partant du sommet 1 et en sortant au sommet 4 .
Par exemple :
• le mot bcbab est un mot reconnu par cet automate, et correspond au chemin 121334;
• le mot abac n’est pas reconnu par cet automate.
1. Parmi les mots suivants, quels sont ceux qui sont reconnus par cet automate ?
abab, abc, abbcbb.
2. Déterminer la matrice d’adjacence M associée au graphe orienté dans laquelle les sommets sont rangés dans l’ordre croissant.
3. Déterminer la matrice M^4 à l’aide de la calculatrice. Combien de mots de 4 lettres sont-ils reconnus par l’automate ? Justifier. Quels sont-ils ?