Sommaire
Activité :
le but de cette activité est exprimer l’équation réduite de la tangente (AM) en utilisant x, y, a , f(a)
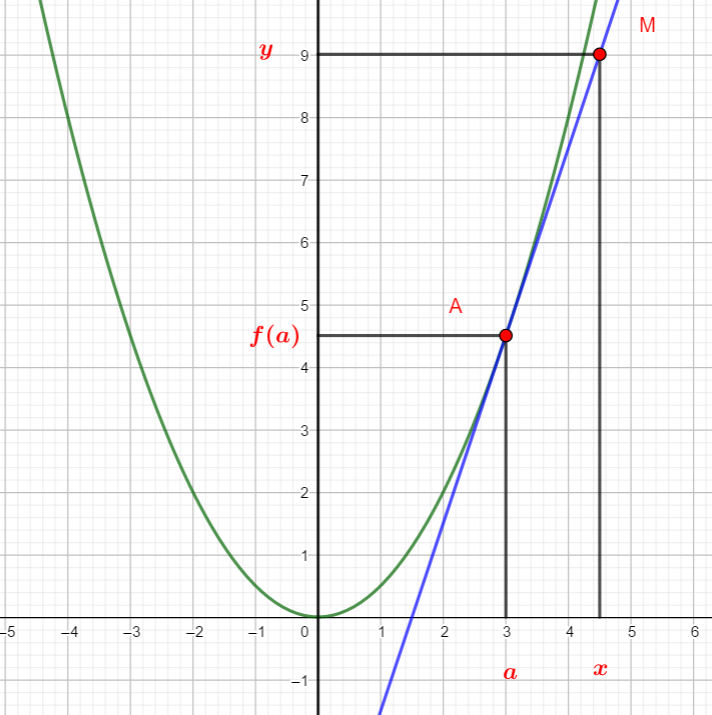
- Déterminer le coefficient directeur de la droite passant par les points A(a;f(a)) et M(x;y) comme on le faisait en classe de seconde.
2. En utilisant le cours de première , exprimer le coefficient directeur de la tangente (AM) à la courbe de la fonction f au point d’abscisse a .
3. Synthèse : en déduire l’équation de la tangente (AM) en utilisant x, y, a , f(a)
Propriété :
L’équation de la tangente à la courbe de la fonction f au point d’abscisse a a pour équation réduite :
y=f'(a)(x-a)+f(a)Comment déterminer l’équation de la tangente à la courbe de la fonction f au point d’abscisse a :
- Je calcule f(a) en remplaçant tous les x par a dans f(x)=…
- Je calcule f'(x) puis je calcule f'(a) en remplaçant tous les x par a dans f'(x)=…
- Je remplace a,f(a),f'(a) par leurs valeurs dans y=f'(a)(x-a)+f(a)
Exercice :
Dans chaque cas, déterminer par le calcul l’équation de la tangente à la courbe de la fonction f au point d’abscisse a.
- f(x)=(x-1)^2 et a=2
2. f(x)=\sqrt{x+1} et a=3
3. f(x)=\frac{5x+1}{x^2+1} et a=0
Comment valider le résultat obtenu pour l’équation de la tangente avec Géogébra :
- Je saisis f(x)=\frac{5x+1}{x^2+1} dans la colonne de gauche, la courbe apparaît sur le graphique;
- Je place A le point de la courbe d’abscisse 0. Pour cela cliquer sur le 2ème onglet en haut à partir de la gauche et sélectionner Point dans le menu déroulant. Cliquer dans le repère sur la courbe au bon endroit.
- Je trace la tangente en A. Pour cela cliquer sur le 4ème onglet en haut à partir de la gauche et sélectionner Tangentes dans le menu déroulant. Cliquer dans le repère sur la courbe et sur le point A. L’équation de la tangente apparaît dans la colonne de gauche.





