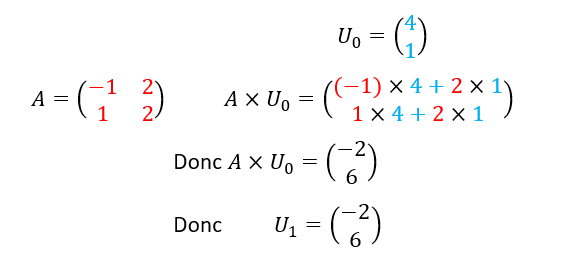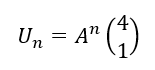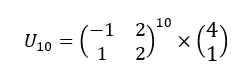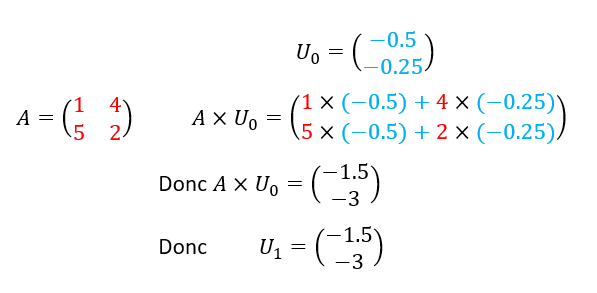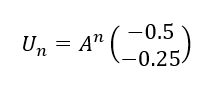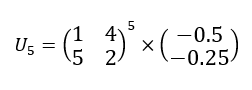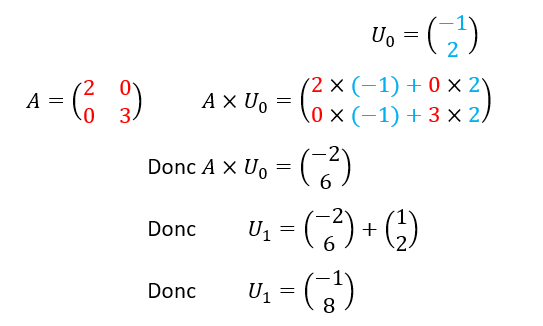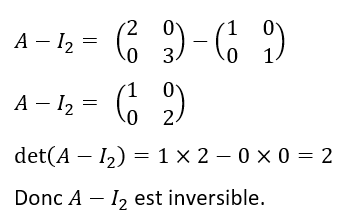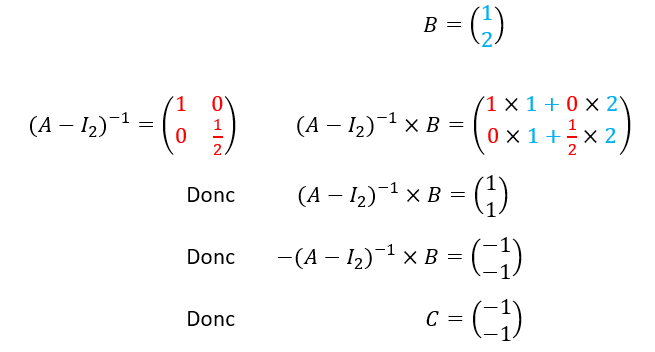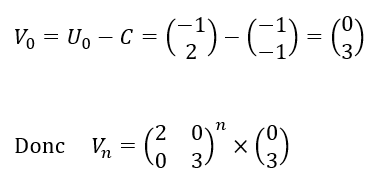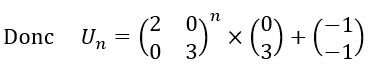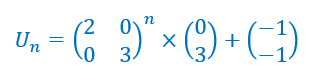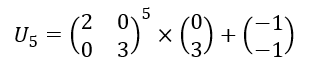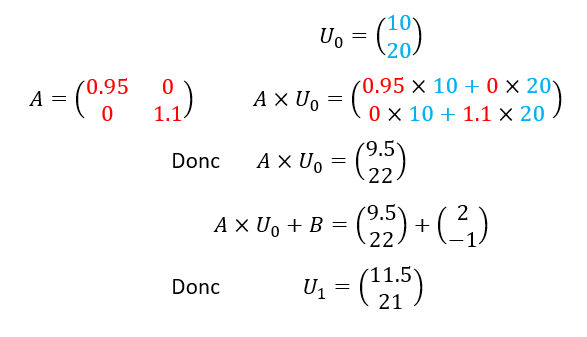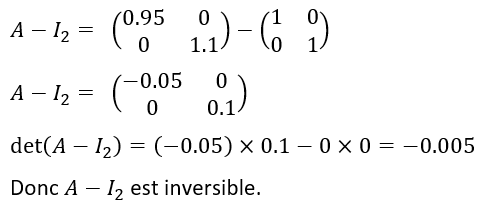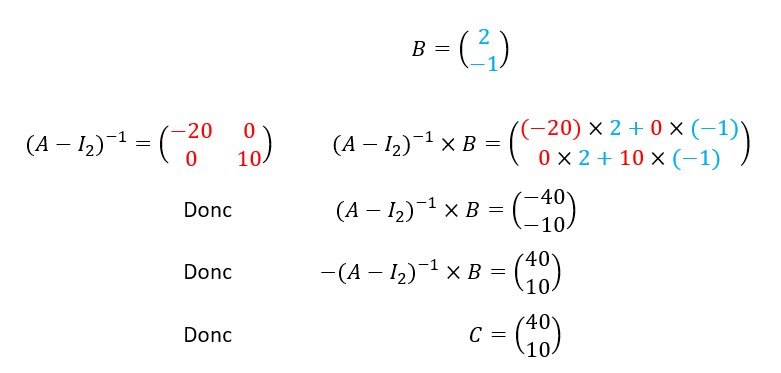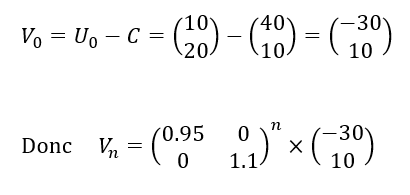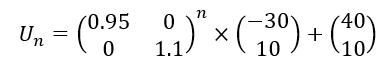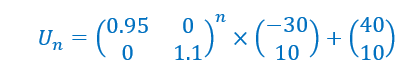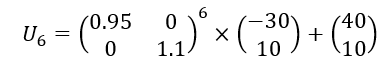Sommaire
Suites de matrices colonnes
Définition
Une suite de matrices colonnes de taille k\times 1 est une fonction qui à tout entier naturel n, associe une matrice colonne de taille k\times 1
Exemples
La suite (U_n) définie pour tout entier naturel n par :
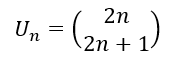
est une suite de matrices colonnes de taille 2\times 1. On a, par exemple :
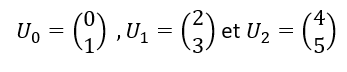
Définition
On dit qu’une suite de matrices (U_n) converge si et seulement si tous ses coefficients convergent. La limite de la suite (U_n) est la matrice dont les coefficients sont les limites des coefficients de la matrice (U_n) .
Exemples
- La suite (U_n) définie pour tout entier naturel n par :
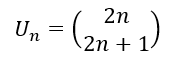
est divergente car lim_{n\to {+\infty}}\hspace{0.25cm}2n=+\infty et lim_{n\to {+\infty}}\hspace{0.25cm}2n+1=+\infty
2. La suite (U_n) définie pour tout entier naturel n non nul par :
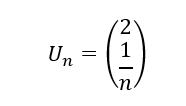
est convergente car lim_{n\to {+\infty}}\hspace{0.25cm}2=2 et lim_{n\to {+\infty}}\hspace{0.25cm}\frac{1}{n}=0.
Sa limite est la matrice
Sa limite est la matrice
Suites de matrices définies par récurrence
Propriété
Soient A une matrice carrée d’ordre p (p est un entier naturel) et (U_n) une suite de matrices colonnes à p lignes telles que pour tout entier naturel n : U_{n+1}=AU_n. Alors pour tout entier naturel n, on a : U_{n}=A^nU_0.
Exemples
- Les suites (a_n) et (b_n) sont deux suites définies par a_0=1 et b_0=0 et pour n\in \mathbf{N}
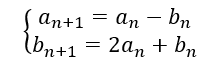
On veut calculer U_5.
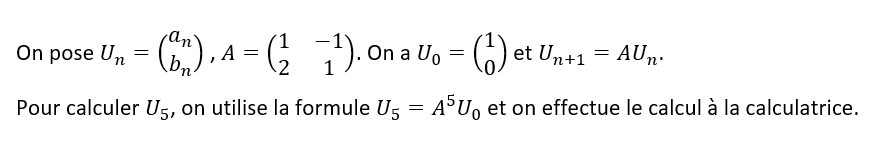
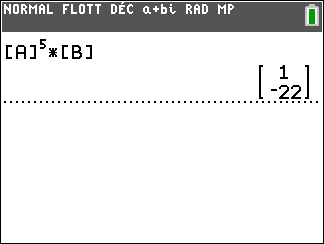
2. La suite (a_n) et (b_n) sont deux suites définies par a_2=1 et b_2=23 et pour n\in \mathbf{N}
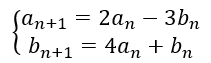
On veut calculer a_0 et b_0.

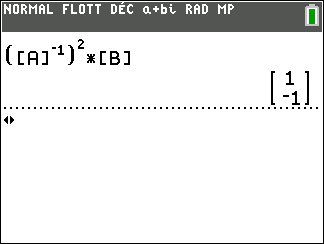
Donc a_0=1 et b_0=-1.
Exercice n°1
Soit la matrice carrée d’ordre 2 suivante
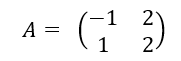
Soit (U_n) la suite de matrices colonnes définie par
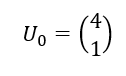
et pour tout n\in \mathbf{N} , U_{n+1}=AU_n
- Calculer U_1.
2. Exprimer pour tout n\in \mathbf{N} , U_{n} en fonction de A et de n.
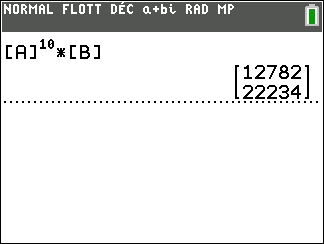
3. A l’aide de la calculatrice, calculer U_{10}.
Exercice n°2
Soit la matrice carrée d’ordre 2 suivante
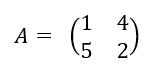
Soit (U_n) la suite de matrices colonnes définie par
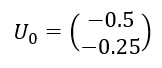
et pour tout n\in \mathbf{N} , U_{n+1}=AU_n
- Calculer U_1.
2. Exprimer pour tout n\in \mathbf{N} , U_{n} en fonction de A et de n.
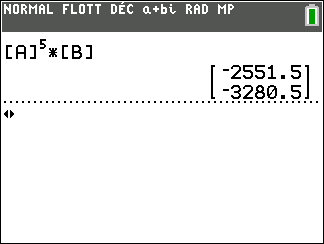
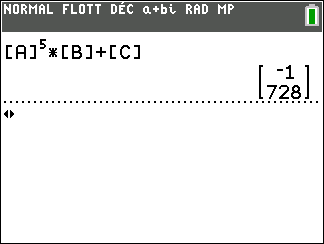
3. A l’aide de la calculatrice, calculer U_{5}.
Propriété
Soient A une matrice carrée d’ordre p (p est un entier naturel) et B une matrice colonne à p lignes et (U_n) une suite de matrices colonnes à p lignes telles que pour tout entier naturel n : U_{n+1}=AU_n+B.
Si la suite (U_n) converge, alors la limite U est une matrice colonne vérifiant U=AU+B.
La matrice U est appelée état stable de la suite (U_n).
Exemple
Soit la suite de matrices colonnes (U_n) définie par U_{n+1}=AU_n+B pour n\in \mathbf{N} avec
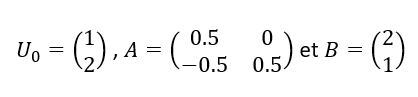
- Déterminer une matrice colonne U telle que U=AU+B.
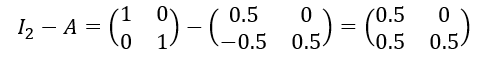
det(I_2-A)=0.5\times 0.5-0.5\times 0=0.25 donc I_2-A est inversible.
Donc U=(I_2-A)^{-1}B
On calcule (I_2-A)^{-1}B à l’aide de la calculatrice.
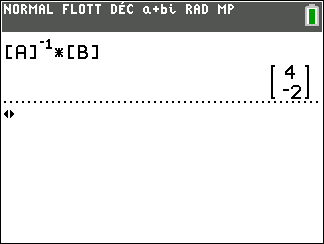
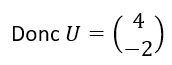
2. On pose V_n=U_n-U. Montrer que, pout tout entier naturel n , V_{n+1}=AV_n. En déduire l’expression de V_n en fonction de n.
4. on exprime V_{n+1} en fonction de U_{n+1}
5. on remplace U_{n+1} par AU_n+B
6. on remplace U par AU+B
3. on développe A(U_{n}-U)
2. on remplace V_{n} par U_{n}-U
1. on écrit la conclusion en bas.
On a montré que V_{n+1}=AV_n donc V_{n}=A^nV_0
3. On admet que pour n\geq 1
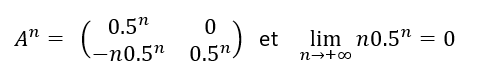
Déduire de ce qui précède l’expression de U_n en fonction de n et étudier sa limite.
On écrit l’égalité dans l’autre sens.
U_n-U=V_n\\U_n=V_n+UOn remplace V_{n} par A^nV_0
U_n=A^nV_0+U
On calcule V_{0}=U_0-U
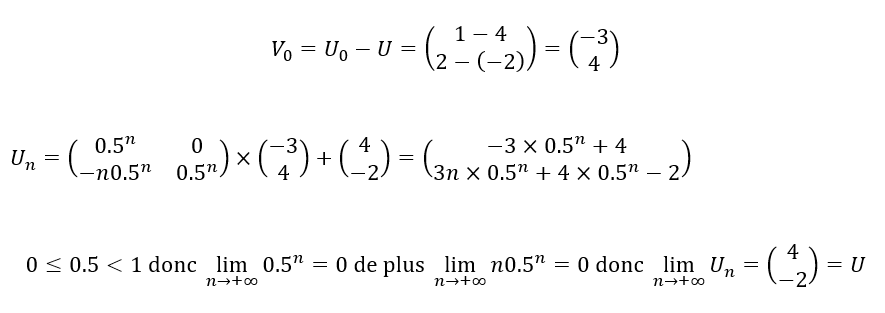
Exercice n°3
Soit (U_n) la suite de matrices colonnes définie par
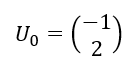
et pour tout n\in \mathbf{N}, U_{n+1}=AU_n+B
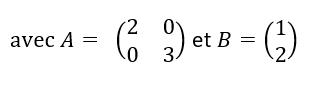
- Calculer U_1.
2.a. Justifier que A-I_2 est inversible.
2.b. Déterminer (A-I_2)^{-1}.
2.c. Calculer C=-(A-I_2)^{-1}B.
3. Montrer que la suite (V_n) définie par pour tout n\in \mathbf{N} , V_{n}=U_n-C vérifie V_{n+1}=AV_n.
4. En déduire (V_n) puis U_n en fonction de n.
5. En déduire U_5.
Exercice n°4
Soit (U_n) la suite de matrices colonnes définie par
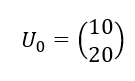
et pour tout n\in \mathbf{N} , U_{n+1}=AU_n+B

- Calculer U_1.
2.a. Justifier que A-I_2 est inversible. Puis déterminer (A-I_2)^{-1}.
2.b. Calculer C=-(A-I_2)^{-1}B.
3. Montrer que la suite (V_n) définie par pour tout n\in \mathbf{N} , V_{n}=U_n-C vérifie V_{n+1}=AV_n.
4. En déduire le terme général de la suite (V_n) en fonction de n. Puis exprimer U_n en fonction de n.
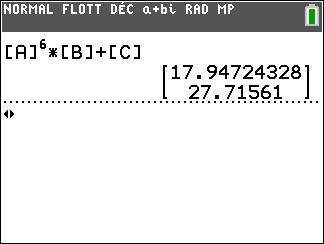
5. En déduire U_{6}.