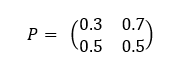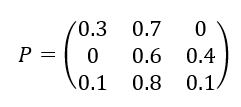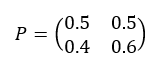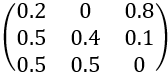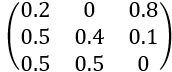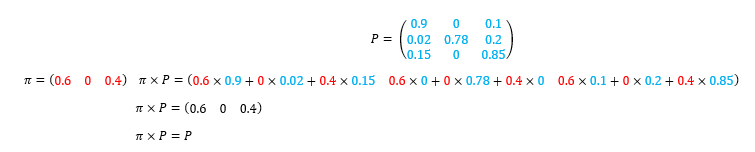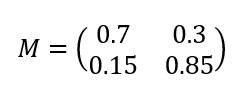Sommaire
Graphe orienté pondéré
Définition
Un graphe orienté est pondéré lorsque chaque arête est affectée d’un nombre réel positif, appelé poids de cette arête.
Un graphe probabiliste est un graphe orienté pondéré où tous les poids sont compris entre 0 et 1 et tel que la somme des poids des arêtes issues d’un même sommet est égale à 1.
Les sommets d’un arbre probabiliste sont appelés des états.
Exemple de graphe probabiliste à trois états
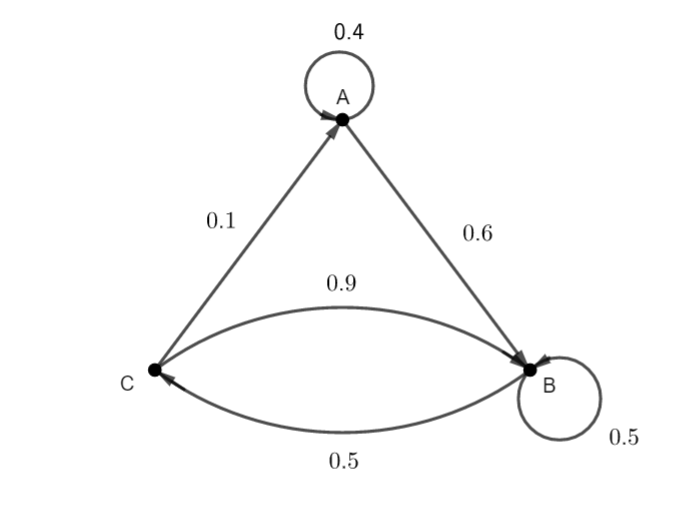
Définition
La matrice associée à un graphe probabiliste comportant p sommets s’appelle une matrice de transition. C’est une matrice carrée d’ordre p où le terme de la i-ème ligne et de la j-ième colonne est égale au poids de l’arête allant du sommet i au sommet j si elle existe, 0 sinon.
Exemple
la matrice de transition de l’exemple précédent est :
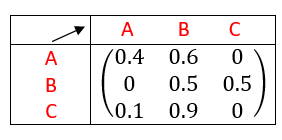
Exercice n°1
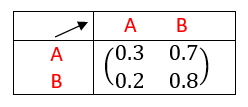
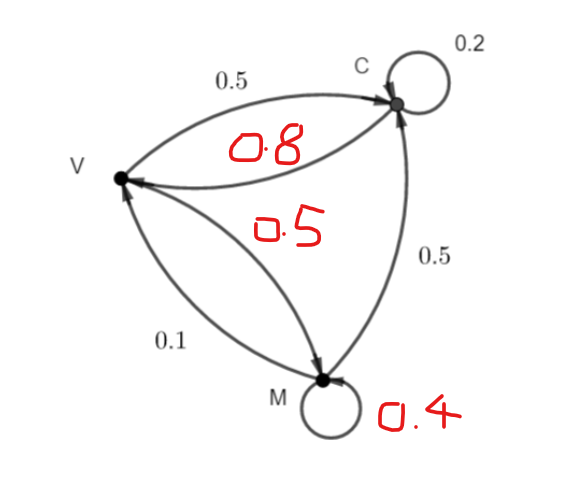
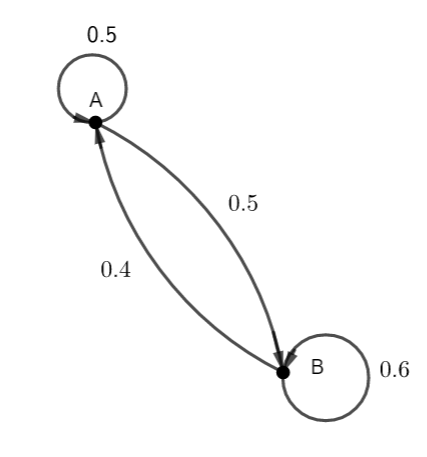
Soit le graphe orienté ci-dessous.
- Vérifier que ce graphe orienté est bien un graphe probabiliste.
2. Déterminer la matrice de transition du graphe probabiliste ci-dessus.
Exercice n°2
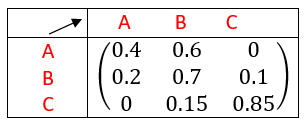
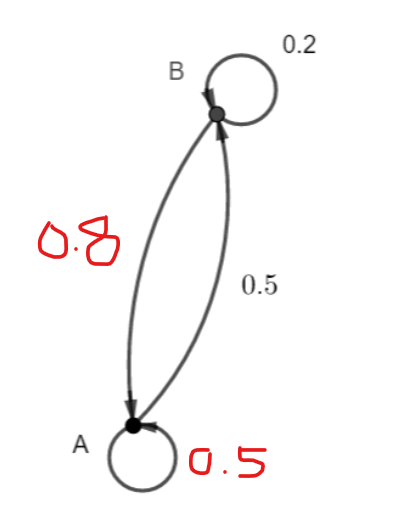
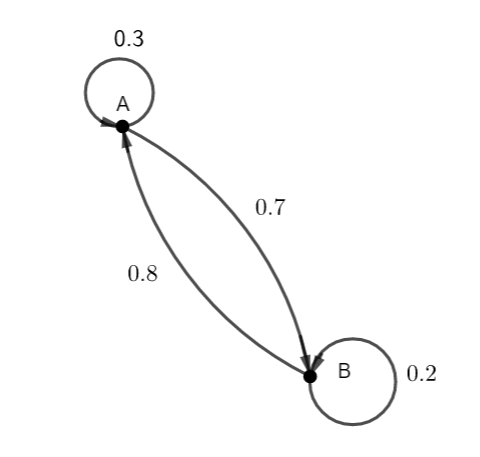
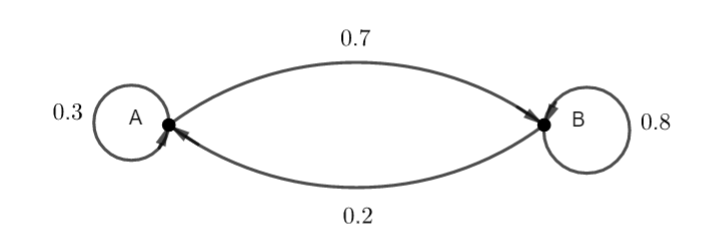
Soit le graphe orienté ci-dessous.
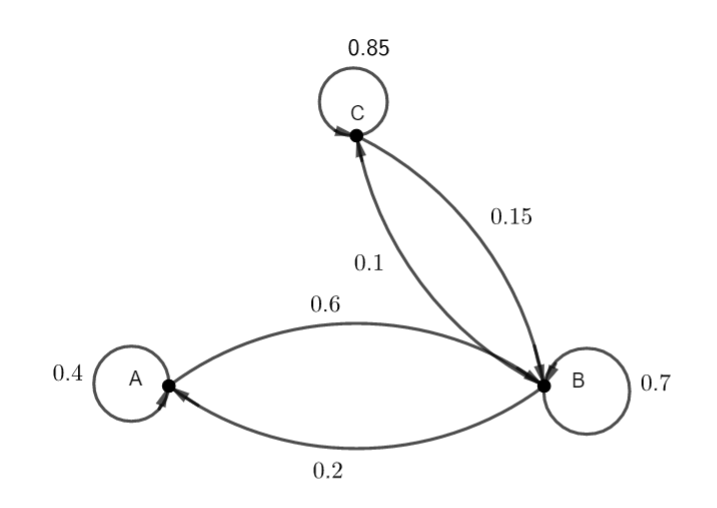
- Vérifier que ce graphe orienté est bien un graphe probabiliste.
2. Déterminer la matrice de transition du graphe probabiliste ci-dessus.
Exercice n°3
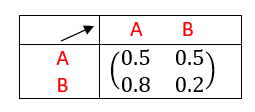
Dans chaque cas, justifier que la matrice P est une matrice de transition, puis représenter le graphe pondéré associé à P
Exercice n°4
1.Recopier et compléter les graphes probabilistes suivants
2.Donner pour chacun des graphes précédents la matrice de transition associée.
Chaîne de Markov à deux ou trois états
Définition
On considère une suite de variables aléatoires (X_n) permettant de modéliser l’évolution par étapes successives d’un système aléatoire comportant différents états.
A l’étape 0, la loi de probabilité de X_0 s’appelle la distribution initiale du système.
A l’étape n, la loi de probabilité de X_n s’appelle la distribution après n transitions.
Lorsque, à chaque étape, la probabilité de transition d’un état à un autre ne dépend pas de n, on dit que la suite (X_n) est une chaîne de Markov.
Exemple : étude d’une marche aléatoire
Une puce se déplace sur les sommets d’un triangle ABC sans rester statique. A chaque saut elle se retrouve sur un autre sommet de manière équiprobable. X_n désigne la position de la puce après n sauts.
Au début de l’expérience, on place la puce en A.
- Donner la distribution initiale du système, c’est-à-dire p(X_0=A), p(X_0=B) et p(X_0=C).
Comme la puce est en A au début de l’expérience,
p(X_0=A)=1, p(X_0=B)=0 et p(X_0=C)=0.
2. A l’aide d’un arbre pondéré, déterminer la distribution du système après deux étapes.
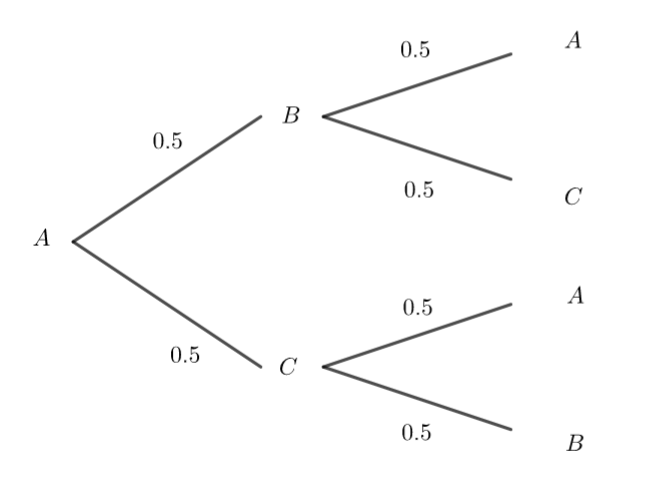
A l’aide de l’arbre pondéré :
p(X_2=A)=0.5\times 0.5+0.5\times 0.5=0.25+0.25=0.5\\p(X_2=B)=0.5\times 0.5=0.25\\p(X_2=C)=0.5\times 0.5=0.253. Expliquer pourquoi la suite (X_n) est une chaîne de Markov et donner le graphe probabiliste et la matrice associée.
(X_n) est une chaîne de Markov car à chaque étape, la probabilité de transition d’un état à un autre ne dépend pas de n.
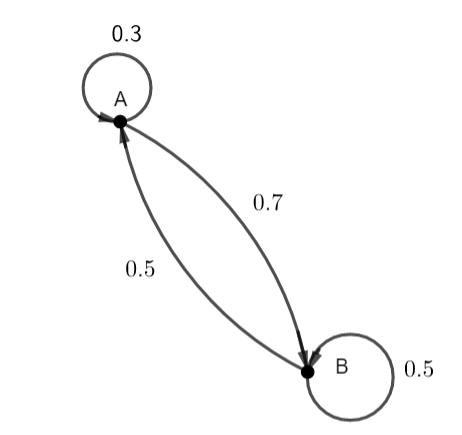
Voici le graphe probabiliste :
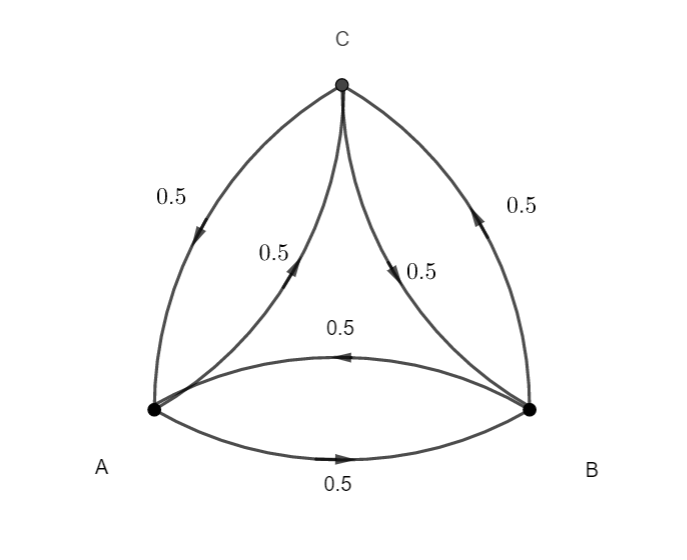
Voici la matrice de transition :
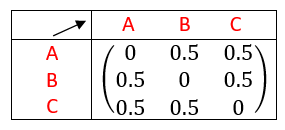
Exercice n°5
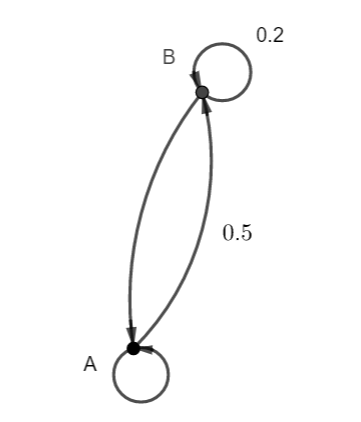
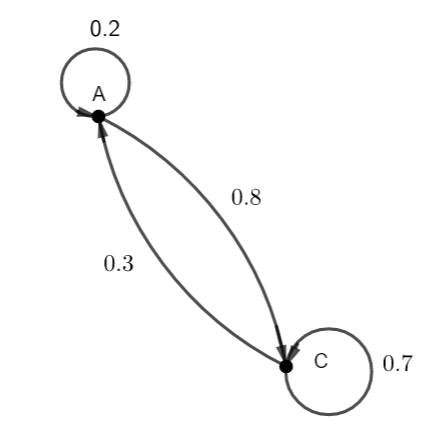
Le chat Matou a pour habitude de dormir soit dans l’armoire (A), soit sur un coussin (C).
- S’il dort une nuit dans l’armoire, la probabilité qu’il dorme dans l’armoire la nuit suivante est 0.2
- S’il dort une nuit sur son coussin, la probabilité qu’il dorme sur son coussin la nuit suivante est 0.7
La première nuit, le matou dort sur son coussin.
- Donner la distribution initiale du système, c’est-à-dire p(X_0=A) et p(X_0=C).
2. Déterminer le graphe pondéré associé.
3. Déterminer la matrice de transition associée.
Modélisation d’une chaîne de Markov à l’aide d’une suite de matrices
Propriété
On considère une chaîne de Markov à 2 ( respectivement 3 ) états et P la matrice de transition associée.
Soient n,i,j trois entiers naturels tels que n\geq1,1\leq i \leq 2 et 1\leq j \leq 2 ( respectivement 1\leq i \leq 3 et 1\leq j \leq 3).
La probabilité de passer de l’état i à l’état j en n étapes est égale au terme de la i-ème ligne et de la j-ième colonne de la matrice P^n.
Exemple : on reprend l’étude de la marche aléatoire de la puce sur les trois sommets du triangle ABC
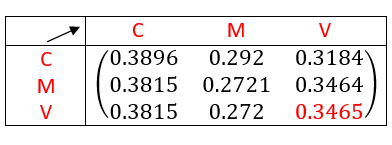
On veut déterminer la probabilité de passer du sommet C au sommet B en 3 étapes.
On calcule le cube de la matrice de transition à l’aide de la calculatrice TI 83 Premium CE
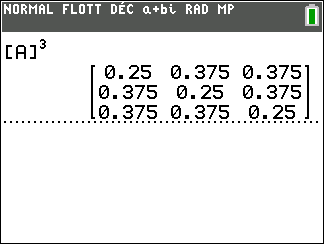
On interprète la matrice en terme de chemins.
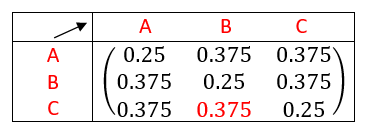
La probabilité de passer du sommet C au sommet B en 3 étapes vaut 0.375.
Exercice n°6
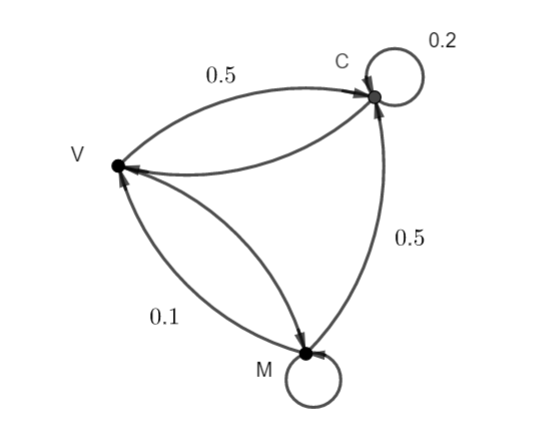
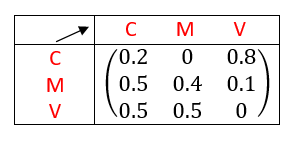
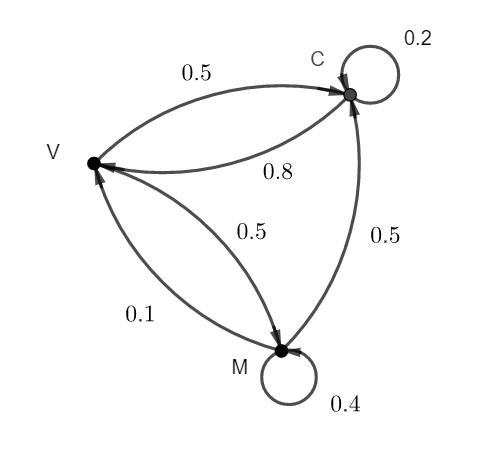
Au cours d’une semaine de pratique sportive, chaque participant a le choix entre trois ateliers : marche (M), vélo (V) ou course à pied (C).
Si le participant a choisi la marche le premier jour : pour le second jour il choisira
- la marche (M) avec une probabilité de 0.4
- le vélo (V) avec une probabilité de 0.1
- la course (C) avec une probabilité de 0.5
Si le participant a choisi le vélo le premier jour : pour le second jour il choisira
- la marche (M) avec une probabilité de 0.5
- la course (C) avec une probabilité de 0.5
Si le participant a choisi la course le premier jour : pour le second jour il choisira
- le vélo (V) avec une probabilité de 0.8
- la course (C) avec une probabilité de 0.2
Au premier jour, Olivier a choisi le vélo.
- Donner la distribution initiale du système, c’est-à-dire p(X_0=M) , p(X_0=V) et p(X_0=C).
2. Déterminer le graphe pondéré associé.
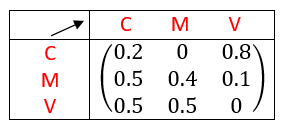
3. Déterminer la matrice de transition associée.
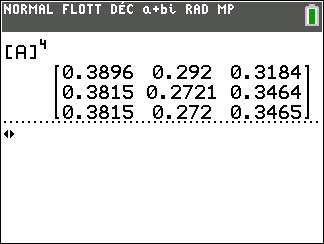
4. Quelle est la probabilité qu’Olivier qui a commencé par le vélo le premier jour fasse du vélo le quatrième jour.
Distribution invariante d’une chaîne de Markov à deux ou trois états
Définition
On considère une chaîne de Markov à 2 ( respectivement 3 ) états et P la matrice de transition associée.
On note \pi_n la matrice ligne à 2 (respectivement 3) colonnes dont le terme de la j-ième colonne est la probabilité qu’à l’étape n la variable aléatoire soit égale à j. C’est-à-dire :
\pi_n=(P(X_n=1) P(X_n=2)) (respectivement \pi_n=(P(X_n=1) P(X_n=2)P(X_n=3)).
Propriété
Pour tout entier naturel n\geq 1 , \pi_{n+1}=\pi_{n}P , \pi_{n}=\pi_{0}P.
S’il existe un entier n tel que la matrice P^n ne contient pas de 0 alors la suite (\pi_n) converge vers la matrice \pi vérifiant \pi=\pi P et cette limite ne dépend pas de \pi_0.
On dit que la matrice \pi représente la distribution invariante du système.
Exemple : déterminer une distribution invariante
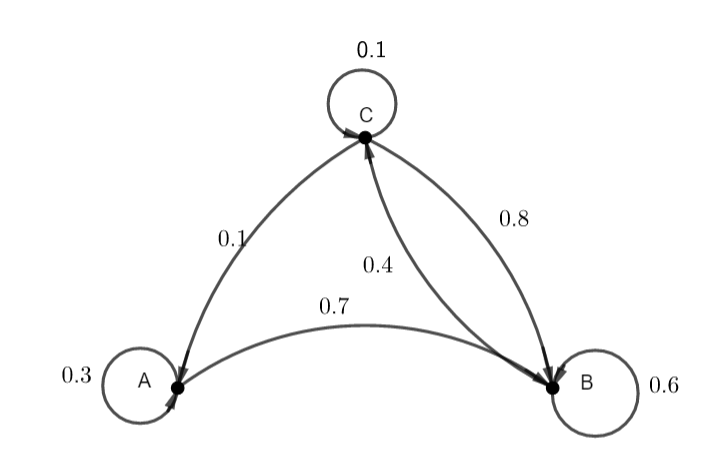
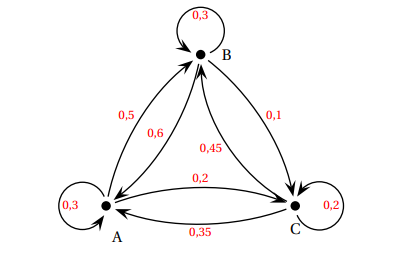
Une ville compte trois collèges A, B et C. le graphe pondéré ci-dessous représentent les évolutions de population entre ces trois collèges d’une année à la suivante.
Exercice n°7
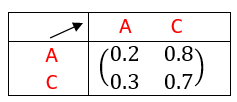
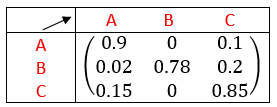
- La matrice P ci-dessous est la matrice de transition associée à une chaîne de Markov
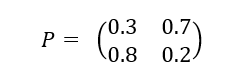
a. Représenter le graphe associé.
b. Déterminer la distribution invariante \pi de cette chaîne.
2. Reprendre la question 1. avec la matrice
Exercice n°8
On considère le graphe probabiliste ci-dessous
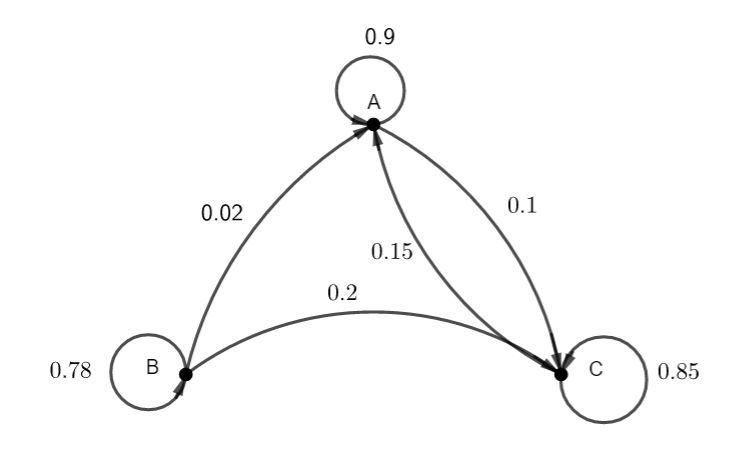
1. Ecrire sa matrice de transition P.
2. Montrer que la matrice ligne \pi=(0.6\hspace{0.4cm}0\hspace{0.4cm}0.4) est une distribution invariante de la chaîne de Markov associée.
Exercice n°9 Liban 2019
Les clients d’un restaurant sont des habitués qui y déjeunent tous les jours. En septembre 2018, le restaurateur propose trois nouveaux plats : plat A, plat B et plat C.
D’un jour à l’autre, il constate que :
• Parmi les clients ayant choisi le plat A : 30% reprennent le plat A le lendemain, 50% prennent le plat B le lendemain.
• Parmi les clients ayant choisi le plat B : 30% reprennent le plat B le lendemain, 60% prennent le plat A le lendemain.
• Parmi les clients ayant choisi le plat C : 35% prennent le plat A le lendemain, 45% prennent le plat B le lendemain.
On note pour tout entier n non nul :
• a_n la proportion de clients ayant choisi le plat A le n-ième jour;
• b_n la proportion de clients ayant choisi le plat B le n-ième jour;
• c_n la proportion de clients ayant choisi le plat C le n-ième jour.
Pour tout entier n\geq 1, on note P_n=(a_n\hspace{0.4cm}b_n\hspace{0.4cm}c_n) l’état probabiliste le n-ième jour.
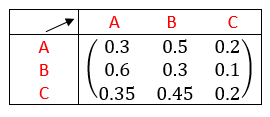
1. Représenter cette situation par un graphe probabiliste.
2. Donner la matrice de transition M de ce graphe, en respectant l’ordre alphabétique des sommets.
3. Le restaurateur a noté que le premier jour 35,5% des clients ont pris le plat A, 40,5% ont pris le plat B et 24% ont pris le plat C.
Calculer P_2.
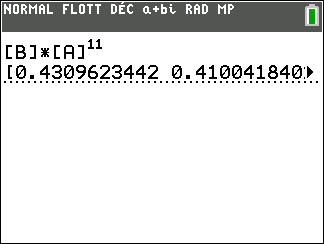
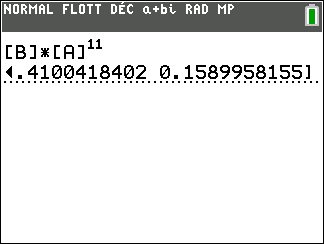
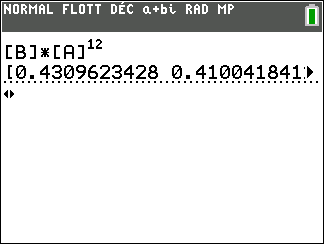
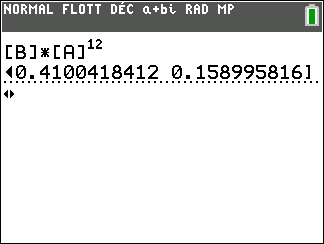
4. Le restaurateur affirme que le douzième jour, la proportion de clients qui choisiront le plat C
sera à peu près la même que le treizième jour, soit environ 15,9%.
A-t-il raison ? Justifier
Exercice n°10 nouvelle calédonie 2019
En 2018, des vélos électriques ont été mis en location. Les clients ont donc eu le choix entre des vélos classiques et des vélos électriques. En 2018, seulement 10% des clients ont loué des vélos électriques.
On admet que tous les clients louent un vélo et que :
• 85% des clients ayant loué un vélo électrique une année en relouent un l’année suivante;
• 70% des clients ayant loué un vélo classique une année en relouent un l’année suivante.
On suppose que le nombre de clients chaque été reste constant. On s’intéresse à la répartition
des clients dans les années à venir.
On note pour tout entier naturel n :
• c_n la probabilité qu’un client pris au hasard choisisse un vélo classique l’année 2018+n;
• e_n la probabilité qu’un client pris au hasard choisisse un vélo électrique l’année 2018+n;
• P_n=(c_n\hspace{0.4cm}e_n)
la matrice correspondant à l’état probabiliste l’année 2018+n.
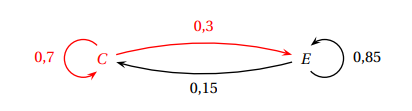
1. Représenter la situation par un graphe probabiliste.
On notera C l’évènement « le client loue un vélo classique » et E l’évènement « le client loue
un vélo électrique »
2. Donner la matrice P_0 traduisant l’état probabiliste initial ainsi que la matrice de transition M en respectant l’ordre des sommets : C d’abord E ensuite.
3. Calculer P_1.
4. Déterminer l’état stable du graphe probabiliste et interpréter le résultat obtenu dans le contexte de l’exercice.